题目内容
△ABC的外接圆的圆心为O,半径为1, ,且
,且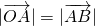 ,则
,则 为
为
- A.1
- B.4π
- C.4π
- D.4π
A
分析:根据 和向量加法的平行四边形法则,知O是BC的中点,由△ABC的外接圆的圆心为O,知BC是圆O的直径,从而求得AB⊥AC,另由
和向量加法的平行四边形法则,知O是BC的中点,由△ABC的外接圆的圆心为O,知BC是圆O的直径,从而求得AB⊥AC,另由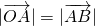 ,可得,∠ABC=60°,故利用向量数量积的定义可以求得
,可得,∠ABC=60°,故利用向量数量积的定义可以求得 .
.
解答:∵△ABC的外接圆的圆心为O,半径为1, ,
,
∴O是BC的中点,且BC是圆O的直径,
∴AB⊥AC,AO=1,BC=2,
∵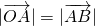
∴AB=1,∴∠ABC=60°,
∴ =1×2×cos60°=1,
=1×2×cos60°=1,
故选A.
点评:此题是个基础题.考查向量在几何中的应用,以及直角三角形有关的性质,同时考查学生灵活应用知识分析解决问题的能力和计算能力.
分析:根据
 和向量加法的平行四边形法则,知O是BC的中点,由△ABC的外接圆的圆心为O,知BC是圆O的直径,从而求得AB⊥AC,另由
和向量加法的平行四边形法则,知O是BC的中点,由△ABC的外接圆的圆心为O,知BC是圆O的直径,从而求得AB⊥AC,另由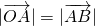 ,可得,∠ABC=60°,故利用向量数量积的定义可以求得
,可得,∠ABC=60°,故利用向量数量积的定义可以求得 .
.解答:∵△ABC的外接圆的圆心为O,半径为1,
 ,
,∴O是BC的中点,且BC是圆O的直径,
∴AB⊥AC,AO=1,BC=2,
∵
∴AB=1,∴∠ABC=60°,
∴
 =1×2×cos60°=1,
=1×2×cos60°=1,故选A.
点评:此题是个基础题.考查向量在几何中的应用,以及直角三角形有关的性质,同时考查学生灵活应用知识分析解决问题的能力和计算能力.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.
已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.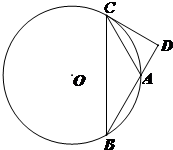 (2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若
(2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若 ,试求直线AB的方程;
,试求直线AB的方程; ,试求s的最大值.
,试求s的最大值.