题目内容
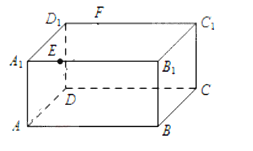
【题目】如图，在棱长为3的正方体ABCD﹣A1B1C1D1中，A1E=CF=1． 
（1）求两条异面直线AC1与D1E所成角的余弦值；
（2）求直线AC1与平面BED1F所成角的正弦值．
【答案】
（1）解：以D为原点，建立空间直角坐标系D﹣xyz如图所示：
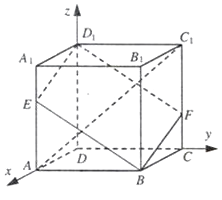
则A（3，0，0），C1=（0，3，3），D1=（0，0，3），E（3，0，2）
∴ 
=（﹣3，3，3）， 
=（3，0，﹣1）
∴cosθ= 
= 
=﹣ 
则两条异面直线AC1与D1E所成角的余弦值为
（2）解：B（3，3，0）， 
=（0，﹣3，2）， =（3，0，﹣1）
设平面BED1F的一个法向量为 
=（x，y，z）
由 
得 
令x=1，则 =（1，2，3）
则直线AC1与平面BED1F所成角的正弦值为
| 
|= 
= 
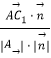【解析】（1）以以D为原点，建立空间直角坐标系D﹣xyz，则我们易求出已知中，各点的坐标，进而求出向量 ， 的坐标．代入向量夹角公式，结合异面直线夹角公式，即可得到答案．（2）设出平面BED1F的一个法向量为 ，根据法向量与平面内任一向量垂直，数量积为0，构造方程组，求出平面BED1F的法向量为 的坐标，代入线面夹角向量公式，即可求出答案．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
