题目内容
在△ABC中，三边a，b，c满足：a2﹣a﹣2b﹣2c=0，a+2b﹣2c+3=0．
（1）探求△ABC的最长边；
（2）求△ABC的最大角．
（1）探求△ABC的最长边；
（2）求△ABC的最大角．
解：（1）∵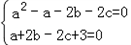
∴
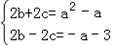即
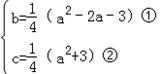
由①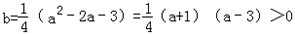
，
∴a＞3，
，
，
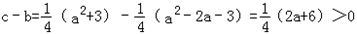所以最大边长为c．
（2）由已知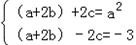
，等式两边对应相乘得（a+2b）2﹣4c2=﹣3a2，
∴a2+b2﹣c2+ab=0，
由余弦定理可知cosC=﹣
，
∴∠C=120°
∴
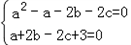
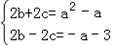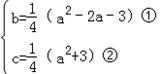
即由①
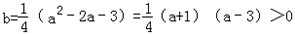，∴a＞3，
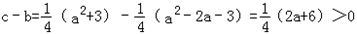，，所以最大边长为c．
（2）由已知
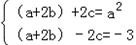，等式两边对应相乘得（a+2b）2﹣4c2=﹣3a2，∴a2+b2﹣c2+ab=0，
由余弦定理可知cosC=﹣
，∴∠C=120°
练习册系列答案
相关题目
在△ABC中，三边a、b、c与面积S的关系是S=
（a2+b2-c2），则角C应为（ ）
| 1 |
| 4 |
| A、30° | B、45° |
| C、60° | D、90° |