题目内容
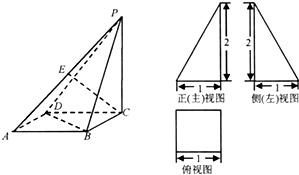 (2010•茂名二模)已知四棱锥P-ABCD的三视图如图所示,其中正(主)视图与侧(左)视为直角三角形,俯视图为正方形.
(2010•茂名二模)已知四棱锥P-ABCD的三视图如图所示,其中正(主)视图与侧(左)视为直角三角形,俯视图为正方形.(1)求四棱锥P-ABCD的体积;
(2)若E是侧棱PA上的动点.问:不论点E在PA的任何位置上,是否都有BD⊥CE?请证明你的结论?
(3)求二面角D-PA-B的余弦值.
分析:(1)根据三视图的数据,结合三视图的特征直接求四棱锥P-ABCD的体积;
(2)若E是侧棱PA上的动点.不论点E在PA的任何位置上,都有BD⊥CE,说明BD⊥平面PAC,都有CE?平面PAC,即可.
(3)在平面DAP过点D作DF⊥PA于F,连接BF.说明∠DFB为二面角D-AP-B的平面角,在△DFB中,求二面角D-PA-B的余弦值.
(2)若E是侧棱PA上的动点.不论点E在PA的任何位置上,都有BD⊥CE,说明BD⊥平面PAC,都有CE?平面PAC,即可.
(3)在平面DAP过点D作DF⊥PA于F,连接BF.说明∠DFB为二面角D-AP-B的平面角,在△DFB中,求二面角D-PA-B的余弦值.
解答: 解:(1)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,
解:(1)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2
∴VP-ABCD=
S正方形ABCD•PC=
×12×2=
.(4分)
(2)不论点E在何位置,都有BD⊥AE(5分)
证明:连接AC,∵ABCD是正方形,
∴BD⊥AC∵PC⊥底面ABCD,且BD?平面ABCD,∴BD⊥PC.(6分)
又∵AC∩PC=C,∴BD⊥平面PAC(7分)
∵不论点E在何位置,都有CE?平面PAC.
∵不论点E在何位置,都有BD⊥CE.(9分)
(3)在平面DAP过点D作DF⊥PA于F,
连接BF∵∠ABP=∠ADP=
,AD=AB=1,
DP=BP=
∴Rt△ADP≌Rt△ABP∴∠PAD=∠PAB,
又AF=AF,AB=AD
从而△ADF≌△ABF,∴BF⊥AP.∴∠DFB为二面角D-AP-B的平面角(12分)
在Rt△ACP中,AP=
=
=
故在Rt△ADP中,DF=
=
=
=BF.
又BD=
,在△DFB中,
由余弦定理得:cos∠BFD=
=-
.
所以二面角D-PA-B的余弦值为-
.(14分)
 解:(1)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,
解:(1)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,且PC=2
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(2)不论点E在何位置,都有BD⊥AE(5分)
证明:连接AC,∵ABCD是正方形,
∴BD⊥AC∵PC⊥底面ABCD,且BD?平面ABCD,∴BD⊥PC.(6分)
又∵AC∩PC=C,∴BD⊥平面PAC(7分)
∵不论点E在何位置,都有CE?平面PAC.
∵不论点E在何位置,都有BD⊥CE.(9分)
(3)在平面DAP过点D作DF⊥PA于F,
连接BF∵∠ABP=∠ADP=
| π |
| 2 |
DP=BP=
| 5 |
又AF=AF,AB=AD
从而△ADF≌△ABF,∴BF⊥AP.∴∠DFB为二面角D-AP-B的平面角(12分)
在Rt△ACP中,AP=
| AC2+PC2 |
(
|
| 6 |
故在Rt△ADP中,DF=
| AD•DP |
| AP |
1×
| ||
|
| ||
| 6 |
又BD=
| 2 |
由余弦定理得:cos∠BFD=
| DF2+BF2-BD2 |
| 2•DF•BF |
| 1 |
| 5 |
所以二面角D-PA-B的余弦值为-
| 1 |
| 5 |
点评:本题是基础题,考查几何体的三视图,几何体的体积的求法,准确判断几何体的形状是解题的关键,同时注意:空间想象能力,逻辑思维能力的培养.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
 (2010•茂名二模)如图所示,椭圆
(2010•茂名二模)如图所示,椭圆