题目内容
设向量a=( sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈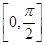 .
.
(1)若|a|=|b|,求x的值;
(2)设函数f(x)=a·b,求f(x)的最大值.
 sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈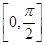 .
.(1)若|a|=|b|,求x的值;
(2)设函数f(x)=a·b,求f(x)的最大值.
(1)x= (2)
(2)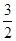
 (2)
(2)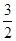
(1)由|a|2=( sin x)2+(sin x)2=4sin2x,
sin x)2+(sin x)2=4sin2x,
|b|2=(cos x)2+(sin x)2=1,
及|a|=|b|,得4sin2x=1.
又x∈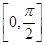 ,从而sin x=
,从而sin x= ,所以x=
,所以x= .
.
(2)f(x)=a·b= sin x·cos x+sin2x
sin x·cos x+sin2x
= sin 2x-
sin 2x- cos 2x+
cos 2x+ =sin
=sin +
+ ,
,
当x∈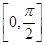 时,-
时,- ≤2x-
≤2x- ≤
≤ π,
π,
∴当2x- =
= 时,
时,
即x= 时,sin
时,sin 取最大值1.
取最大值1.
所以f(x)的最大值为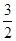 .
.
 sin x)2+(sin x)2=4sin2x,
sin x)2+(sin x)2=4sin2x,|b|2=(cos x)2+(sin x)2=1,
及|a|=|b|,得4sin2x=1.
又x∈
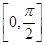 ,从而sin x=
,从而sin x= ,所以x=
,所以x= .
.(2)f(x)=a·b=
 sin x·cos x+sin2x
sin x·cos x+sin2x=
 sin 2x-
sin 2x- cos 2x+
cos 2x+ =sin
=sin +
+ ,
,当x∈
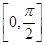 时,-
时,- ≤2x-
≤2x- ≤
≤ π,
π,∴当2x-
 =
= 时,
时,即x=
 时,sin
时,sin 取最大值1.
取最大值1.所以f(x)的最大值为
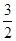 .
.
练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 sin(
sin(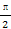 +
+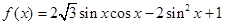 .
.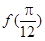 的值;
的值; 在区间
在区间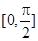 上的最大值和最小值.
上的最大值和最小值.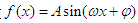 (其中
(其中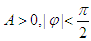 )的图象如图所示,把函数
)的图象如图所示,把函数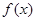 的图像向右平移
的图像向右平移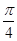 个单位,再向下平移1个单位,得到函数
个单位,再向下平移1个单位,得到函数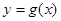 的图像.
的图像.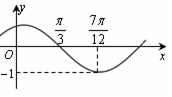
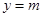 与函数
与函数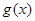 图像在
图像在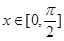 时有两个公共点,其横坐标分别为
时有两个公共点,其横坐标分别为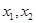 ,求
,求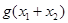 的值;
的值;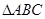 内角
内角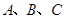 的对边分别为
的对边分别为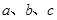 ,且
,且
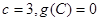 .若向量
.若向量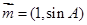 与
与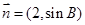 共线,求
共线,求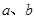 的值.
的值.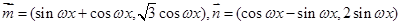 ,且
,且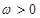 ,
,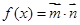 ,
,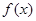 的图象相邻两对称轴之间的距离等于
的图象相邻两对称轴之间的距离等于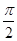 .
.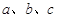 分别为角
分别为角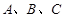 的对边,
的对边,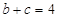 ,
,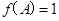 ,求△ABC面积的最大值.
,求△ABC面积的最大值. ,
,  ,则
,则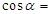 。
。 是
是 边
边 延长线上一点,记
延长线上一点,记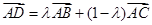 . 若关于
. 若关于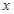 的方程
的方程 在
在 上恰有两解,则实数
上恰有两解,则实数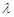 的取值范围是( )
的取值范围是( )
 或
或
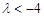 或
或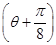 =
=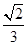 ,求tan θ的值.
,求tan θ的值.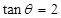 ,则
,则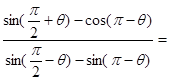 .
.