题目内容
已知函数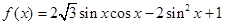 .
.
(Ⅰ)求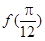 的值;
的值;
(Ⅱ)求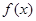 在区间
在区间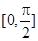 上的最大值和最小值.
上的最大值和最小值.
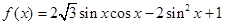 .
.(Ⅰ)求
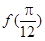 的值;
的值;(Ⅱ)求
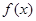 在区间
在区间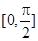 上的最大值和最小值.
上的最大值和最小值.(Ⅰ) ;(Ⅱ)
;(Ⅱ)
 ;(Ⅱ)
;(Ⅱ)
试题分析:(Ⅰ)可直接将角代入求值,也可先用正弦、余弦二倍角公式和化一公式将此函数化简为正弦型函数,再代入角求值。(Ⅱ)根据
 的范围先求整体角的范围,再根据三角函数图像求其值域。
的范围先求整体角的范围,再根据三角函数图像求其值域。试题解析:解:(Ⅰ)由
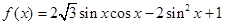
 ,
,得
 .
.所以
 . 8分
. 8分(Ⅱ)因为
 ,
,所以
 .
. 当
 ,即
,即 时,
时,函数
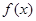 在区间
在区间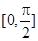 上的最大值为
上的最大值为 .
.当
 ,即
,即 时,
时,函数
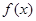 在
在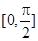 上的最小值为
上的最小值为 . 13分
. 13分
练习册系列答案
相关题目
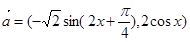 ,
,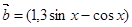 ,
,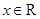 ,函数
,函数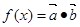 .
.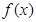 的最小正周期;
的最小正周期;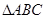 中,角
中,角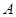 、
、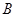 、
、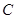 所对的边分别为
所对的边分别为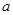 、
、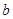 、
、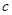 ,
,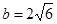 ,
,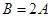 ,
,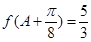 ,求
,求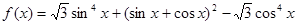 .
.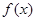 的最小值及取最小值时
的最小值及取最小值时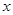 的集合;
的集合;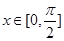 时的值域;
时的值域;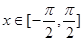 时的单调递减区间.
时的单调递减区间. 中,
中, 且
且 .
. 的大小;
的大小; ,求
,求 的值.
的值. )来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )
)来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( ) sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈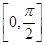 .
.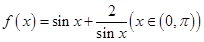 的最小值是
的最小值是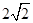 ;②在
;②在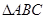 中,若
中,若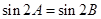 ,则
,则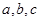 满足
满足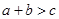 ,则
,则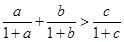 ;④如果
;④如果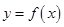 是可导函数,则
是可导函数,则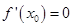 是函数
是函数 在直线
在直线 上,则
上,则 的值等于 。
的值等于 。
 的值域为 .
的值域为 .