题目内容
已知△ABC的两边长分别为AB=25,AC=39,且O为△ABC外接圆的圆心.(注:39=3×13,65=5×13)(1)若外接圆O的半径为
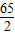 ,且角B为钝角,求BC边的长;
,且角B为钝角,求BC边的长;(2)求
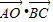 的值.
的值.
【答案】分析:(1)由正弦定理求得sinB= ,sinC=
,sinC=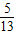 ,从而求得 cosC=
,从而求得 cosC=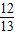 ,cosB=-
,cosB=- .再利用两角和的正弦公式求得 sin(B+C) 的值,利用正弦定理求得BC的值.
.再利用两角和的正弦公式求得 sin(B+C) 的值,利用正弦定理求得BC的值.
(2)把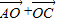 =
=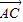 平方,再把
平方,再把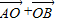 =
=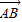 平方,相减可得 2
平方,相减可得 2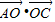 -2
-2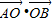 =896,即 2
=896,即 2 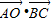 =896,从而求得
=896,从而求得 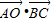 的值.
的值.
解答:解:(1)由正弦定理有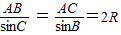 ,把AB=25,AC=39,外接圆O的半径为
,把AB=25,AC=39,外接圆O的半径为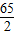 ,且角B为钝角代入求得sinB=
,且角B为钝角代入求得sinB= ,sinC=
,sinC=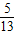 ,
,
∴cosC=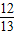 ,cosB=-
,cosB=- ,∴sin(B+C)=sinBcosC+cosBsinC=
,∴sin(B+C)=sinBcosC+cosBsinC=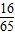 .
.
再由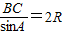 ,∴BC=2RsinA=65sin(B+C)=16.
,∴BC=2RsinA=65sin(B+C)=16.
(2)∵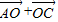 =
=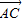 ,∴
,∴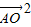 +
+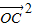 +2
+2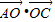 =
=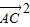 =392,
=392,
同理,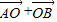 =
=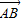 ,∴
,∴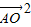 +
+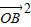 +2
+2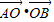 =
=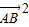 =252,
=252,
两式相减可得 2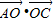 -2
-2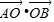 =896,
=896,
即 2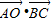 =896,∴
=896,∴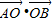 =448.
=448.
点评:本题主要考查两个向量的数量积的定义,正弦定理、两角和的正弦公式的应用,属于中档题.
 ,sinC=
,sinC=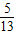 ,从而求得 cosC=
,从而求得 cosC=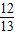 ,cosB=-
,cosB=- .再利用两角和的正弦公式求得 sin(B+C) 的值,利用正弦定理求得BC的值.
.再利用两角和的正弦公式求得 sin(B+C) 的值,利用正弦定理求得BC的值.(2)把
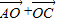 =
=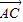 平方,再把
平方,再把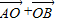 =
=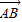 平方,相减可得 2
平方,相减可得 2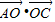 -2
-2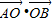 =896,即 2
=896,即 2 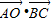 =896,从而求得
=896,从而求得 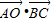 的值.
的值.解答:解:(1)由正弦定理有
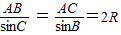 ,把AB=25,AC=39,外接圆O的半径为
,把AB=25,AC=39,外接圆O的半径为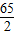 ,且角B为钝角代入求得sinB=
,且角B为钝角代入求得sinB= ,sinC=
,sinC=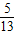 ,
,∴cosC=
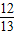 ,cosB=-
,cosB=- ,∴sin(B+C)=sinBcosC+cosBsinC=
,∴sin(B+C)=sinBcosC+cosBsinC=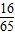 .
.再由
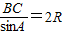 ,∴BC=2RsinA=65sin(B+C)=16.
,∴BC=2RsinA=65sin(B+C)=16.(2)∵
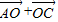 =
=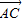 ,∴
,∴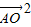 +
+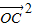 +2
+2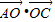 =
=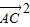 =392,
=392,同理,
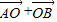 =
=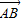 ,∴
,∴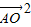 +
+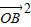 +2
+2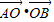 =
=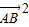 =252,
=252,两式相减可得 2
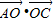 -2
-2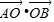 =896,
=896,即 2
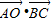 =896,∴
=896,∴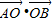 =448.
=448.点评:本题主要考查两个向量的数量积的定义,正弦定理、两角和的正弦公式的应用,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
已知△ABC的两边长分别为AB=25,AC=39,且O为△ABC外接圆的圆心.(注:39=3×13,65=5×13)
(1)若外接圆O的半径为
,且角B为钝角,求BC边的长;
(2)求
•
的值.
(1)若外接圆O的半径为
| 65 |
| 2 |
(2)求
| AO |
| BC |
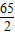 ,且角B为钝角,求BC边的长;
,且角B为钝角,求BC边的长;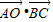 的值.
的值. ,且角B为钝角,求BC边的长;
,且角B为钝角,求BC边的长;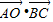 的值.
的值.