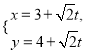Question

【题目】已知椭圆的短轴长为，离心率为.

（Ⅰ）求椭圆的标准方程;

（Ⅱ）设椭圆的左，右焦点分别为，左，右顶点分别为，，点，，为椭圆上位于轴上方的两点，且，直线的斜率为，记直线，的斜率分别为，，求的值.

Answer 1

【答案】（Ⅰ）；（Ⅱ）0.

【解析】

（Ⅰ）由题意，得2b，，结合隐含条件即可求得a，b的值，则椭圆方程可求；（Ⅱ）由（Ⅰ），可知A（﹣3，0），B（3，0），F1（﹣1，0），求得F1M的方程为，记直线F1M与椭圆的另一交点为M′，设M（x1，y1）（y1＞0），M′（x2，y2），得N（﹣x2，﹣y2），联立直线方程与椭圆方程，求得M，N的坐标，代入斜率公式求解．

（Ⅰ）由题意，得，.

又，∴，，.

∴椭圆C的标准方程为.

（Ⅱ）

由（Ⅰ），可知，，.

据题意，直线的方程为.

记直线与椭圆的另一交点为，设，.

∵，根据对称性，得.

联立，消去，得.

∵，∴，.

∵，，

∴，即的值为0.