题目内容
设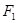 、
、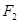 分别为椭圆
分别为椭圆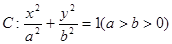 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ) 若椭圆C上的点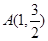 到
到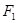 、
、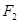 两点的距离之和等于4, 写出椭圆C的方程和离心率.;
两点的距离之和等于4, 写出椭圆C的方程和离心率.;
(Ⅱ) 若M、N是椭圆C上关于原点对称的两点,点P是椭圆上除M、N外的任意一点, 当直线PM、PN的斜率都存在, 并记为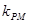 、
、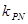 时, 求证:
时, 求证: 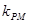 ·
·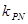 为定值.
为定值.
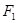 、
、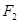 分别为椭圆
分别为椭圆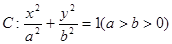 的左、右两个焦点.
的左、右两个焦点.(Ⅰ) 若椭圆C上的点
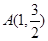 到
到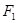 、
、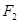 两点的距离之和等于4, 写出椭圆C的方程和离心率.;
两点的距离之和等于4, 写出椭圆C的方程和离心率.;(Ⅱ) 若M、N是椭圆C上关于原点对称的两点,点P是椭圆上除M、N外的任意一点, 当直线PM、PN的斜率都存在, 并记为
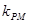 、
、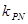 时, 求证:
时, 求证: 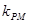 ·
·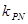 为定值.
为定值.(1) 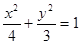 ,
,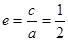
(2)

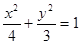 ,
,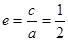
(2)


试题分析:解:(Ⅰ) 根据已知条件: 2a="4," 即a=2, (1 分)
∴椭圆方程为
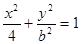 . ( 2 分)
. ( 2 分)又
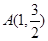 为椭圆C上一点, 则
为椭圆C上一点, 则 , ( 3 分)
, ( 3 分)解得
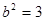 , 则 椭圆C的方程为
, 则 椭圆C的方程为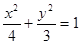 . ( 4 分)
. ( 4 分)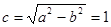 , ( 5 分)
, ( 5 分)则椭圆C的离心率.
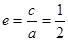 ( 6 分)
( 6 分)(Ⅱ) 设
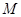 、
、 是椭圆上关于原点对称点, 设
是椭圆上关于原点对称点, 设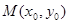 , 则
, 则 ,
,P点坐标为(x, y), 则
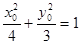 , ( 8 分)
, ( 8 分)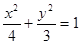 ( 9 分)
( 9 分)即
 ,
,  (10 分)
(10 分) ( 11 分)
( 11 分)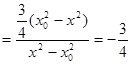 (13 分)
(13 分)点评:考查了直线与椭圆的位置关系的运用,解决的关键是利用韦达定理来求解,属于基础题。

练习册系列答案
相关题目
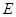 :
: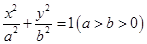 的一个焦点为
的一个焦点为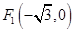 且过点
且过点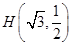 .
.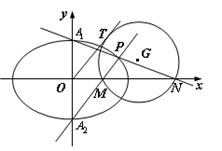
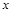 轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.
轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.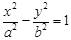 (a>0,b>0) 的左、右焦点,过F1的直线与
(a>0,b>0) 的左、右焦点,过F1的直线与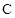 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
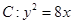 的焦点为
的焦点为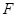 ,准线与
,准线与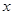 轴的交点为
轴的交点为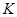 ,点
,点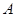 在
在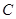 上且
上且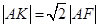 ,则
,则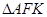 的面积为
的面积为 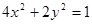 的一个焦点
的一个焦点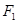 的直线与椭圆交于
的直线与椭圆交于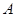 、
、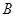 两点,则
两点,则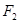 构成
构成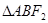 ,那么
,那么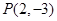 是双曲线
是双曲线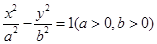 上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________.
上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________.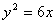 上,O为坐标原点,则
上,O为坐标原点,则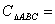 ( )
( )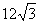
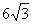
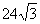
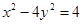 有共同的渐近线,且经过点
有共同的渐近线,且经过点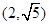 的双曲线方程是 .
的双曲线方程是 .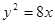 相切倾斜角为
相切倾斜角为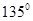 的直线
的直线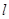 与
与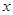 轴和
轴和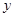 轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线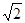 C.2 D.
C.2 D.