题目内容
已知椭圆
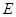 :
: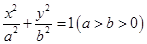 的一个焦点为
的一个焦点为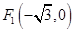 且过点
且过点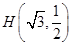 .
.
(Ⅰ)求椭圆E的方程;
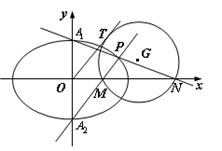
(Ⅱ)设椭圆E的上下顶点分别为A1,A2,P是椭圆上异于A1,A2的任一点,直线PA1,PA2分别交
 轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.
轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
(Ⅰ) .(Ⅱ)线段
.(Ⅱ)线段 的长为定值
的长为定值 .
.
 .(Ⅱ)线段
.(Ⅱ)线段 的长为定值
的长为定值 .
.试题分析:(Ⅰ) 由题意得
 ,
, ,解得
,解得 ,
,所以椭圆
 的方程为
的方程为 .
.(Ⅱ)由(Ⅰ)可知
 ,设
,设 ,其中
,其中 ,
,直线
 :
: ,令
,令 ,得
,得 ;
;直线
 :
: ,令
,令 ,得
,得 .
.设圆
 的圆心为
的圆心为 ,半径为
,半径为 ,
,则

 ,
, ,
,

而
 ,所以
,所以 ,所以
,所以 ,
,所以
 ,即线段
,即线段 的长为定值
的长为定值 .
.点评::从近几年课标地区的高考命题来看,解析几何综合题主要考查直线和圆锥曲线的位置关系以及范围、最值、定点、定值、存在性等问题,直线与多种曲线的位置关系的综合问题将会逐步成为今后命题的热点,尤其是把直线和圆的位置关系同本部分知识的结合,将逐步成为今后命题的一种趋势

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
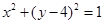 ,曲线C2:
,曲线C2: ,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则
,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则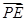 ·
·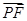 的最小值为 ( )
的最小值为 ( )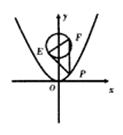
 :
: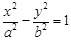
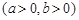 的离心率
的离心率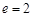 ,过双曲线
,过双曲线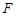 作
作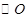 :
: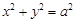 的两条切线,切点分别为
的两条切线,切点分别为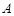 、
、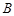 ,则
,则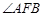 的大小等于( )
的大小等于( ) =4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=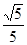
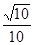
 =16x
=16x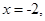 则抛物线的方程是( )
则抛物线的方程是( ) 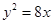
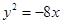
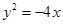
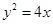
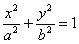
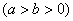 的离心率是
的离心率是 ,则双曲线
,则双曲线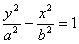 的渐近线方程是( )
的渐近线方程是( )
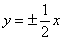


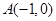 和
和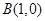 ,动点
,动点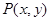 在直线
在直线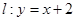 上移动,椭圆
上移动,椭圆 以
以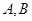 为焦点且经过点
为焦点且经过点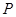 ,记椭圆
,记椭圆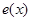 ,则函数
,则函数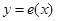 的大致图像是( )
的大致图像是( )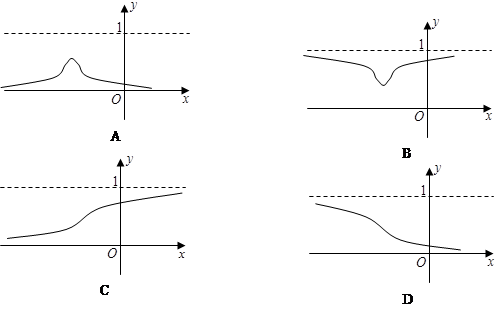
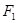 、
、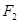 分别为椭圆
分别为椭圆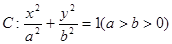 的左、右两个焦点.
的左、右两个焦点.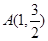 到
到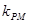 、
、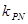 时, 求证:
时, 求证: