题目内容
已知△OAB的顶点O（0，0）、A（2，0）、B（3，2），OA边上的中线所在直线为l．
（Ⅰ）求l的方程；
（Ⅱ）求点A关于直线l的对称点的坐标．
（Ⅰ）求l的方程；
（Ⅱ）求点A关于直线l的对称点的坐标．
分析：（I）求出线段OA的中点坐标，利用两点式方程求出l的方程；
（II）设出点A关于直线l的对称点的坐标，通过AA′与对称轴方程的斜率乘积为-1，以及AA′的中点在对称轴上，得到方程组，求出对称点的坐标．
（II）设出点A关于直线l的对称点的坐标，通过AA′与对称轴方程的斜率乘积为-1，以及AA′的中点在对称轴上，得到方程组，求出对称点的坐标．
解答：解：（I）线段OA的中点为（1，0），
于是中线方程为
=
，
即y=x-1；
（II）设对称点为A′（a，b），
则
，
解得
，
即A′（1，1）．
于是中线方程为
| y-2 |
| 2-0 |
| x-3 |
| 3-1 |
即y=x-1；
（II）设对称点为A′（a，b），
则
|
解得
|
即A′（1，1）．
点评：本题是中档题，考查直线方程的求法，对称点的坐标的求法，考查计算能力．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
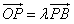，点Q是边AB上一点，且
。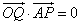