题目内容
已知点A∈{（x，y）|-1≤x≤1，-1≤y≤1}，点B（2，1），则
•
最小值为（ ）
| OA |
| OB |
分析：作出可行域、目标函数，经过平移即可找出目标函数取得最小值时的位置，可求出其最小值．
解答：解：根据A∈{（x，y）|-1≤x≤1，-1≤y≤1}，作出其可行域：
则
•
=（2，1）•（x，y）=2x+y，
令2x+y=t，则y=-2x+t，画出目标函数l，
由图象可知：当直线l过点（-1，-1）时，2x+y=t取得最小值，
tmin=2×（-1）+（-1）=-3．
故选B．
则
| OA |
| OB |
令2x+y=t，则y=-2x+t，画出目标函数l，
由图象可知：当直线l过点（-1，-1）时，2x+y=t取得最小值，
tmin=2×（-1）+（-1）=-3．
故选B．
点评：正确画出可行域、目标函数并求出取得最小值时的位置是解题的关键．
练习册系列答案
相关题目
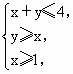过点P的直线l与圆C：x2＋y2＝14相交于A、B两点，则|AB|的最小值是
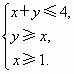过点P的直线l与圆C：x2＋y2＝14交于A、B两点，那么|AB|的最小值是________
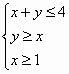，过点P的直线l与圆C∶x2＋y2＝14相交于A、B两点，则AB的最小值为________．
，0 )和曲线y =
（2 ≤ x ≤ 2
，
)，求n的最大值。
(x≠0,y≠0)上的动点,F1、F2为椭圆的两个焦点,O是坐标原点,若M是∠F1PF2的角平分线上一点,且
,则|
|的取值范围是
) C.［2
,3) D.［0,4］