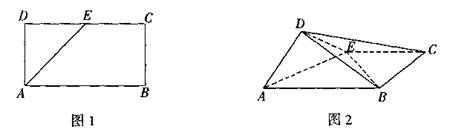Question

如图1，矩形ABCD中，AB=2AD=2a，E为DC的中点，现将△ADE沿AE折起，使平面ADE⊥平面ABCE，如图2．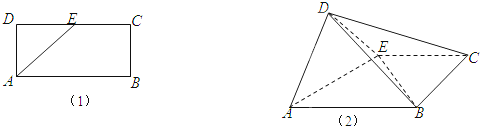

（1）求四棱锥D-ABCE的体积；
（2）求证：AD⊥平面BDE．

Answer 1

分析：（1）先取AE中点O，连接DO，推得DO⊥平面ABCE．即DO为高，然后再分别求出高和低面积即可．
（2）先证AE⊥EB，再利用DO⊥平面ABCE?DO⊥BE?BE⊥平面ADE?BE⊥AD，又有AD⊥DE，可得结论．

解答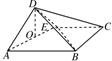：解：（1）取AE中点O，连接DO，由题意知：
AB=2AD=2a，ED=EC，
∴AD=DE，∴DO⊥AE，
又∵平面ADE⊥平面ABCE，
∴DO⊥平面ABCE．
在等腰Rt△ADE中，
AD=DE=a，
DO=

2

2

a，
又S_梯形ABCE=

1

2

（a+2a）a=

3

2

a²，
∴V_D-ABCE=

1

3

S_梯形ABCE•DO=

1

3

•

3

2

a²•

2

2

a=

2

4

a³．

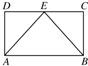（2）证明：在题图1中，连接BE，
则BE=

a2+a2

=

2

a，
又AE=

2

a，AB=2a，
∴AB²=AE²+EB²，
∴AE⊥EB，
由（1）知：DO⊥平面ABCE，
∴DO⊥BE，又DO∩AE=O，
∴BE⊥平面ADE
∴BE⊥AD
又∵AD⊥DE，
∴AD⊥平面BDE．

点评：本题考查平面和平面垂直的判定和性质以及棱锥的体积计算．在证明面面垂直时，其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直