Question

（09年山东质检）（12分）

如图1，矩形ABCD中，AB=2AD=2a，E为DC的中点，现将△ADE沿AE折起，使平面ADE⊥平面ABCE，如图2．

   （I）求二面角A―BC―D的正切值；

 

   （Ⅱ）求证：AD⊥平面BDE．

 

 

 

 

 

 

 

 

 

Answer 1

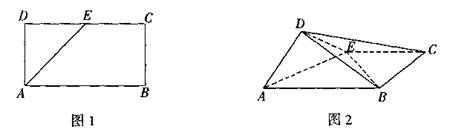
解析：（Ⅰ）取AE中点O，BC中点F，连结DO，OF，DF（如图）

由题知：AB=2AD，DE=EC,

,

又,

,……………………………………………………………2分

又,

,

由三垂线定理得，

………………………………………4分

在，

即二面角A―BC―D的正切值是……………………………………6分

（Ⅱ）在图1中，连结BE，则，

又，

……………………………………8分

由（Ⅰ）知平面ABCE，

，

，…………………………………………………………10分

，

又，

…………………………………………………………12分