题目内容
5.在党的群众教育路线总结阶段,一督导组从某单位随机抽调25名员工,对本单位的各项开展工作进行打分评价,现获得如下的数据:70,82,81,76,80,77,77,65,85,69,83,71,76,89,74,73,83,82,72,74,86,79,76,根据上述数据得到样本的频率分布表如下:| 分组 | 频数 | 频率 |
| [65,70] | 3 | 0.12 |
| (70,75] | 5 | 0.20 |
| (75,80] | n | x |
| (80,85] | 7 | y |
| (85,90] | m | 0.08 |
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布表,求在该单位中任取3名员工的打分,恰有2名员工的打分在(75,85)的概率.
分析 (1)根据频率分布表,利用频率、频数与样本容量的关系求出m、n与x、y的值;
(2)根据频率分布表,画出样本频率分布直即可;
(3)根据样本频率分布表,计算在(75,85)中的人数,求出基本事件数和对应的概率.
解答 解:(1)根据频率分布表,得;
$\frac{m}{0.08}$=$\frac{3}{0.12}$,
解得m=2;
所以n=25-3-5-7-2=8,
x=$\frac{8}{25}$=0.32,
y=$\frac{7}{25}$=0.28;
(2)根据上述频率分布表,画出样本频率分布直方图如下;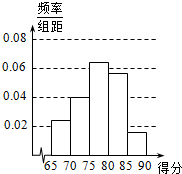
(3)根据样本频率分布表,得;
在(75,85)中的频率为0.32+0.28=0.60,
所以在(75,85)的人数为25×0.60=15;
在该单位25名员工中任取3人,基本事件是${C}_{25}^{3}$种,
其中有2人在(75,80]的基本事件数是${C}_{15}^{2}$•${C}_{10}^{1}$,
所以,所求的概率为P=$\frac{{C}_{15}^{2}{•C}_{10}^{1}}{{C}_{25}^{3}}$=$\frac{21}{46}$.
点评 本题考查了频率分布直方图的应用问题,也考查了古典概型的概率应用问题,是基础题目.

练习册系列答案
相关题目
15.在R上定义运算?:x?y=x(1-y),若对任意x>2,不等式(x-2)?x<a+2恒成立,则实数a的取值范围是( )
| A. | $(-\frac{7}{4},+∞)$ | B. | [-2,+∞) | C. | (-∞,-2] | D. | $[-2,-\frac{7}{4})$ |
20.已知集合A={x|-3<x<5,且x∈Z},B={x|x2-x-2>0},则A∩B=( )
| A. | {0,1} | B. | {-1,0} | C. | {-2,3,4} | D. | {2,3,4} |
10.函数f(x)=sin(πcos x)在区间[0,2π]上的零点个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.若$\overrightarrow{AO}+\overrightarrow{OB}+\overrightarrow{CA}+\overrightarrow{OC}+\overrightarrow{BO}$=( )
| A. | $\overrightarrow{AB}$ | B. | $\overrightarrow 0$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{BC}$ |