题目内容
在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=
,则A到A1BD的距离为( )
| 3 |
分析:先确定△A1BD的面积,再利用VA1-ABD=VA-A1BD可得A到A1BD的距离.
解答:解:由题意,△A1BD中,A1B=A1D=2,BD=
,∴△A1BD的面积为
×
×
=
设A到A1BD的距离为h,则由VA1-ABD=VA-A1BD可得
×
×1×1×
=
×
×h
∴h=
故选A.
| 2 |
| 1 |
| 2 |
| 2 |
4-
|
| ||
| 2 |
设A到A1BD的距离为h,则由VA1-ABD=VA-A1BD可得
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
∴h=
| ||
| 7 |
故选A.
点评:本题考查点到面的距离的计算,解题的关键是利用等体积转化,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点. 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.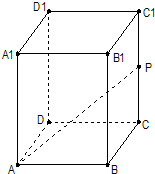 (2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)
(2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)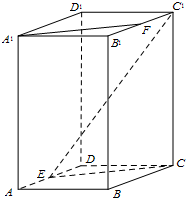 (2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.
(2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.