题目内容
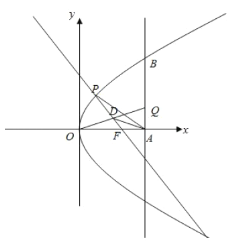
【题目】如图，在平面直角坐标系xoy中，椭圆C：
的左顶点为A，点B是椭圆C上异于左、右顶点的任一点，P是AB的中点，过点B且与AB垂直的直线与直线OP交于点Q，已知椭圆C的离心率为
，点A到右准线的距离为6．
（1）求椭圆C的标准方程；
（2）设点Q的横坐标为
，求的取值范围．
【答案】（1）
（2）
（4,8）
【解析】
（1）首先根据题意得到
，又因为点A到右准线的距离为6，得到
＝6，联立求得
＝2，c＝1，根据椭圆中
的关系，求得b的值，从而求得椭圆的方程；
（2）设出直线AB的方程，之后与椭圆方程联立，得到
，从而求得
，从而得到OP的斜率，进一步求得直线OP的方程，再得出BQ的方程，两直线方程联立，求得
，从而得到其范围.
（1）依题意，有：
，即，
又＝6，所以，
＝6，解得：＝2，c＝1，
b＝
＝
，
所以，椭圆C的方程为：
，
（2）由（1）知：A（-2,0），设AB：
，即，
则 
，
练习册系列答案
阅读快车系列答案
相关题目
【题目】某小店每天以每份5元的价格从食品厂购进若干份食品，然后以每份10元的价格出售.如果当天卖不完，剩下的食品还可以每份1元的价格退回食品厂处理.
(Ⅰ)若小店一天购进16份，求当天的利润
（单位：元）关于当天需求量
（单位：份，
）的函数解析式；
(Ⅱ)小店记录了100天这种食品的日需求量（单位：份），整理得下表：
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)小店一天购进16份这种食品，
表示当天的利润（单位：元），求的分布列及数学期望；
(ii)以小店当天利润的期望值为决策依据，你认为一天应购进食品16份还是17份？
