Question

【题目】设常数．在平面直角坐标系中，已知点，直线：，曲线：．与轴交于点、与交于点．、分别是曲线与线段上的动点．

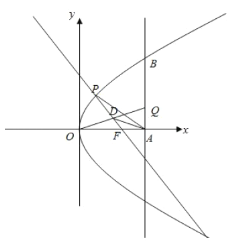
（1）用表示点到点距离；

（2）设，，线段的中点在直线，求的面积；

（3）设，是否存在以、为邻边的矩形，使得点在上？若存在，求点的坐标；若不存在，说明理由．

Answer 1

【答案】（1）；（2）；（3）见解析.

【解析】

（1）方法一：设B点坐标，根据两点之间的距离公式，即可求得|BF|；

方法二：根据抛物线的定义，即可求得|BF|；

（2）根据抛物线的性质，求得Q点坐标，即可求得OD的中点坐标，即可求得直线PF的方程，代入抛物线方程，即可求得P点坐标，即可求得△AQP的面积；

（3）设P及E点坐标，根据直线kPFkFQ=﹣1，求得直线QF的方程，求得Q点坐标，根据+=，求得E点坐标，则（）2=8（+6），即可求得P点坐标．

（1）方法一：由题意可知：设，

则，

∴；

方法二：由题意可知：设，

由抛物线的性质可知：，∴；

（2），，，则，

∴，∴，设的中点，

，

，则直线方程：，

联立，整理得：，

解得：，（舍去），

∴的面积；

（3）存在，设，，则，，

直线方程为，∴，，

根据，则，

∴，解得：，

∴存在以、为邻边的矩形，使得点在上，且．