题目内容
(本题满分18分,第(1)小题9分,第(2)小题9分)
设复数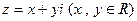 与复平面上点
与复平面上点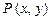 对应.
对应.
(1)设复数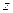 满足条件
满足条件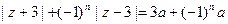 (其中
(其中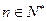 ,常数
,常数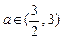 ),当
),当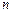 为奇数时,动点
为奇数时,动点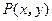 的轨迹为
的轨迹为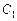 ;当
;当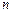 为偶数时,动点
为偶数时,动点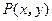 的轨迹为
的轨迹为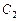 ,且两条曲线都经过点
,且两条曲线都经过点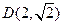 ,求轨迹
,求轨迹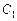 与
与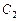 的方程;
的方程;
(2)在(1)的条件下,轨迹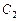 上存在点
上存在点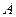 ,使点
,使点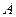 与点
与点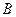
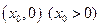 的最小距离不小于
的最小距离不小于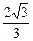 ,求实数
,求实数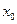 的取值范围.
的取值范围.
设复数
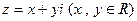 与复平面上点
与复平面上点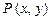 对应.
对应.(1)设复数
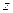 满足条件
满足条件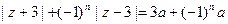 (其中
(其中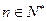 ,常数
,常数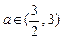 ),当
),当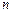 为奇数时,动点
为奇数时,动点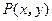 的轨迹为
的轨迹为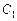 ;当
;当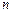 为偶数时,动点
为偶数时,动点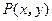 的轨迹为
的轨迹为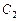 ,且两条曲线都经过点
,且两条曲线都经过点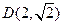 ,求轨迹
,求轨迹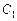 与
与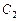 的方程;
的方程;(2)在(1)的条件下,轨迹
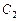 上存在点
上存在点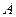 ,使点
,使点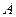 与点
与点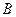
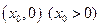 的最小距离不小于
的最小距离不小于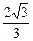 ,求实数
,求实数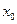 的取值范围.
的取值范围.(1)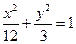
(2)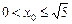 或
或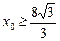 .
.
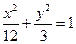
(2)
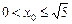 或
或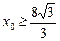 .
.(本题满分18分,第(1)小题9分,第(2)小题9分)
解:(1)方法1:①当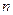 为奇数时,
为奇数时,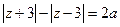 ,常数
,常数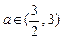 ,
,
轨迹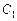 为双曲线,其方程为
为双曲线,其方程为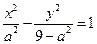 ;……3分
;……3分
②当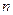 为偶数时,
为偶数时,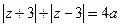 ,常数
,常数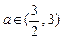 ,
,
轨迹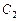 为椭圆,其方程为
为椭圆,其方程为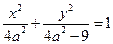 ;……6分
;……6分
依题意得方程组
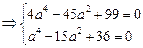 解得
解得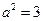 ,
,
因为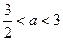 ,所以
,所以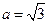 ,
,
此时轨迹为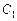 与
与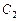 的方程分别是:
的方程分别是: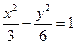
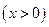 ,
,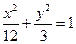 .……9分
.……9分
方法2:依题意得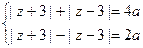
 ……3分
……3分
轨迹为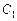 与
与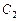 都经过点
都经过点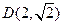 ,且点
,且点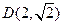 对应的复数
对应的复数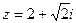 ,
,
代入上式得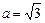 ,……6分
,……6分
即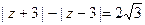 对应的轨迹
对应的轨迹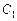 是双曲线,方程为
是双曲线,方程为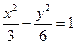
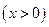 ;
;
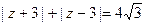 对应的轨迹
对应的轨迹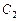 是椭圆,方程为
是椭圆,方程为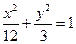 .……9分
.……9分
(2)由(1)知,轨迹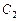 :
: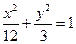 ,设点
,设点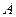 的坐标为
的坐标为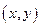 ,
,
则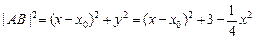
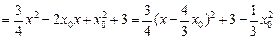 ,
, ……12分
……12分
当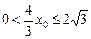 即
即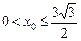 时,
时,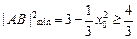
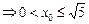
当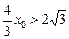 即
即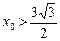 时,
时,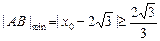
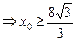 ,……16分
,……16分
综上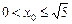 或
或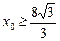 .……18分
.……18分
解:(1)方法1:①当
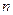 为奇数时,
为奇数时,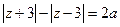 ,常数
,常数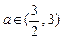 ,
,轨迹
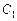 为双曲线,其方程为
为双曲线,其方程为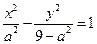 ;……3分
;……3分②当
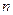 为偶数时,
为偶数时,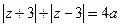 ,常数
,常数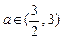 ,
,轨迹
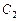 为椭圆,其方程为
为椭圆,其方程为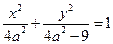 ;……6分
;……6分依题意得方程组

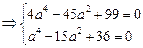 解得
解得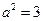 ,
,因为
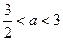 ,所以
,所以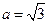 ,
,此时轨迹为
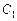 与
与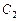 的方程分别是:
的方程分别是: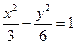
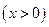 ,
,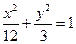 .……9分
.……9分方法2:依题意得
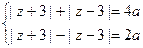
 ……3分
……3分轨迹为
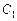 与
与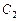 都经过点
都经过点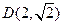 ,且点
,且点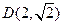 对应的复数
对应的复数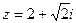 ,
,代入上式得
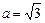 ,……6分
,……6分即
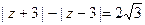 对应的轨迹
对应的轨迹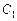 是双曲线,方程为
是双曲线,方程为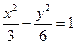
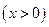 ;
;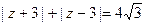 对应的轨迹
对应的轨迹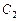 是椭圆,方程为
是椭圆,方程为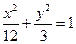 .……9分
.……9分(2)由(1)知,轨迹
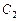 :
: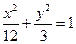 ,设点
,设点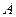 的坐标为
的坐标为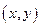 ,
,则
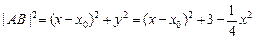
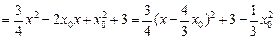 ,
, ……12分
……12分当
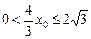 即
即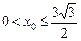 时,
时,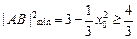
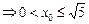
当
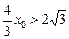 即
即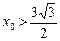 时,
时,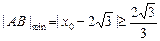
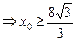 ,……16分
,……16分综上
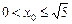 或
或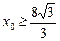 .……18分
.……18分
练习册系列答案
相关题目
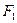 、
、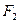 分别是椭圆
分别是椭圆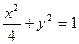 的左、右焦点.
的左、右焦点.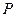 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求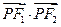 的最大值和最小值;
的最大值和最小值;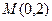 的直线
的直线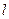 与椭圆交于不同的两点
与椭圆交于不同的两点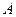 、
、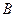 ,且∠
,且∠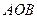 为钝角(其中
为钝角(其中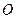 为坐标原点),求直线
为坐标原点),求直线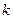 的取值范围.
的取值范围.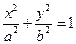 上一点
上一点 及其焦点
及其焦点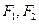 满足
满足

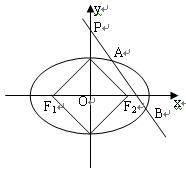
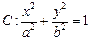
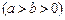 的一个焦点
的一个焦点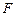 且垂直于
且垂直于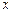 轴的直线交椭圆于点
轴的直线交椭圆于点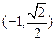 。
。 求椭圆C的方程;
求椭圆C的方程;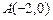 的直线
的直线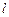 与椭圆
与椭圆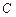 交于两点
交于两点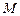 、
、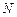 ,使得
,使得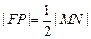 (其中
(其中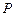 为弦
为弦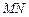 的中点)?若存在,求出直线
的中点)?若存在,求出直线
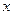 轴上的椭圆与
轴上的椭圆与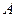 ,与
,与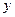 轴的正半轴交于点
轴的正半轴交于点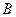 ,
,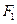 是左焦点且
是左焦点且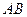 的距离
的距离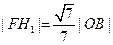 ,求椭圆的离心率.
,求椭圆的离心率.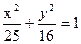 的离心率为
的离心率为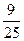
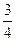
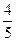 .m
.m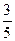
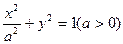 的一条准线经过抛物线
的一条准线经过抛物线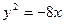 的焦点,则该椭圆的离心率为 ( )
的焦点,则该椭圆的离心率为 ( )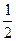
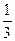

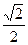
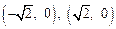 ,则PC·PD的最大值为 ( )
,则PC·PD的最大值为 ( )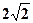 C 3 D
C 3 D