题目内容
在直角坐标系中,A (3,0),B (0,3),C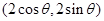
(1)若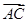 ^
^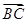 ,求
,求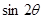 的值;
的值;
(2)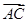 与
与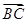 能否共线?说明理由。
能否共线?说明理由。
(1) =
= ;(2)不能共线。得
;(2)不能共线。得 =
= >1,矛盾!
>1,矛盾!
解析试题分析: ,
, 1分
1分
(1) Þ
Þ 2分
2分
Þ
Þ 4分
4分
两边平方得 1+ =
= 得
得 =
= 6分
6分
(2)不能共线。 8分
理由如下:
若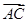 、
、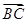 共线,则有
共线,则有
解得 10分
10分
两边平方得 1+ =
= 得
得 =
= >1,矛盾! 12分
>1,矛盾! 12分
考点:本题主要考查平面向量的坐标运算、数量积,向量垂直及共线的条件,和差倍半的三角函数公式。
点评:中档题,本题综合考查平面向量的坐标运算、数量积,向量垂直及共线的条件,和差倍半的三角函数公式。总的看解答思路明确,注重了基础知识的考查,是一道好题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 与
与 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 等于
等于
A. | B. | C. | D.4 |
 中,满足:
中,满足: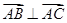 ,
, 是
是 的中点.
的中点.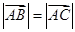 ,求向量
,求向量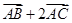 与向量
与向量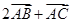 的夹角的余弦值;
的夹角的余弦值; 是
是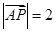 ,且
,且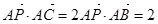 ,求
,求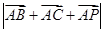 的最小值.
的最小值.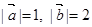 ,且
,且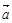 与
与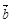 的夹角为120°.
的夹角为120°.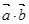 ; (2)
; (2) 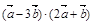 ; (3)
; (3) 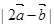 .
.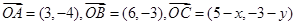 .
.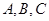 三点共线,求
三点共线,求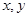 应满足的条件;
应满足的条件;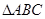 为等腰直角三角形,且
为等腰直角三角形,且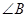 为直角,求
为直角,求 和点
和点 ,其中
,其中 ,若
,若 ,求
,求 得值。
得值。 ,
,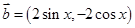 ,
,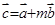 ,
, ,
,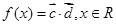 .
. 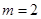 时,求
时,求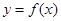 的取值范围;
的取值范围;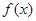 的最大值是
的最大值是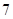 ,求实数
,求实数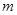 的值;
的值; 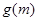 ,对任意的
,对任意的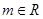 ,都有
,都有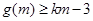 恒成立,求实数
恒成立,求实数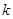 的取值范围.
的取值范围.  的坐标.
的坐标. |=3,|
|=3,| |=2,且3
|=2,且3