题目内容

在△ABC中，三边a,b,c满足(a+b+c)(a+b-c)=ab,求tanC.

解:∵(a+b+c)(a+b-c)=(a+b)2-c2=a2+b2-c2+2ab=,

∴a2+b2-c2=.

则cosC=.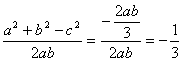

∵0＜∠C＜π,

∴sinC=

于是tanC=

练习册系列答案
相关题目
在△ABC中，三边a、b、c与面积S的关系是S=
1
4
（a2+b2-c2），则角C应为（　　）
A、30°B、45°
C、60°D、90°
在△ABC中，三边a、b、c所对的角分别为A、B、C，已知a=2
3
，b=2，△ABC的面积S=
3
，则C=
π
6
或
5π
6
π
6
或
5π
6
．
在△ABC中，三边a，c，b成等差，则sinA的范围是
[
3
2
，1）
[
3
2
，1）
．
在△ABC中，三边a、b、c与面积S的关系式为S=
1
4
（a2+b2-c2），则角C=
π
4
π
4
．
在△ABC中，三边a，b，c成等差数列，B=30°，三角形ABC的面积为
1
2
，则b的值是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网