Question

【题目】如图，正方体中，E为AB中点，F在线段上.给出下列判断：①存在点F使得平面；②在平面内总存在与平面平行的直线；③平面与平面ABCD所成的二面角（锐角）的大小与点F的位置无关；④三棱锥的体积与点F的位置无关.其中正确判断的有（ ）

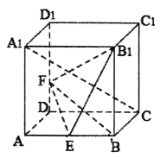
A.①②B.③④C.①③D.②④

Answer 1

【答案】D

【解析】

运用线面垂直的定义，结合反证法即可判断①；运用线面平行的判定定理，即可判断②；由二面角的平面角的定义，结合向量法即可判断③；由线面平行，结合三棱锥的体积公式可以判断④．

对于①，假设存在F使得⊥平面，则⊥，又⊥，∩＝，∴⊥平面，则⊥，这与⊥矛盾，所以①错误；

对于②，因为平面与平面相交，设交线为，则在平面内与平行的直线平行于平面，故②正确；

对于③，以点为坐标原点，以所在直线为轴，所在直线为轴，所在直线为轴，建立空间坐标系，则平面的法向量为而平面的法向量，随着位置变化，故平面与平面所成的二面角（锐角）的大小与点的位置有关，故③错误；

对于④，三棱锥的体积即为三棱锥，因为∥平面，所以，当在线段上移动时，到平面的距离不变，故三棱锥的体积与点的位置无关，即④正确．

故选：D．