题目内容
双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.已知|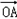 |、|
|、|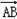 |、|
|、|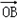 |成等差数列,且
|成等差数列,且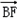 与
与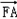 同向.
同向.
(1)求双曲线的离心率;
(2)设AB被双曲线所截得的线段的长为4,求双曲线的方程.
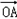 |、|
|、|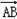 |、|
|、|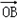 |成等差数列,且
|成等差数列,且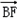 与
与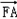 同向.
同向.(1)求双曲线的离心率;
(2)设AB被双曲线所截得的线段的长为4,求双曲线的方程.
解:(1)设双曲线方程为
由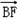 ,
,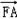 同向,
同向,
∴渐近线的倾斜角为(0,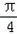 ),
),
∴渐近线斜率为:
∴|AB|2=(|OB|﹣|OA|)(|OB|+|OA|)=(|OB|﹣|OA|)2|AB|,∴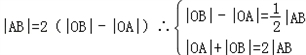
∴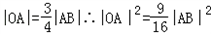
可得: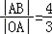 ,
,
而在直角三角形OAB中,注意到三角形OAF也为直角三角形,即tan∠AOB=
而由对称性可知:OA的斜率为k=tan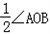
∴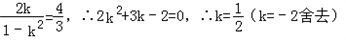 ;
;
∴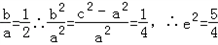 ∴
∴
(2)由第(1)知,a=2b,可设双曲线方程为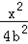 ﹣
﹣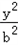 =1,c=
=1,c=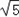 b,
b,
∴AB的直线方程为 y=﹣2(x﹣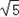 b),
b),
代入双曲线方程得:15x2﹣32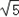 bx+84b2=0,
bx+84b2=0,
∴x1+x2=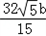 ,x1x2=
,x1x2=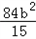 ,
,
4=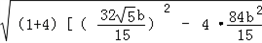 ,16=
,16=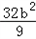 ﹣
﹣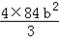 ,
,
∴b2=9,所求双曲线方程为: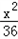 ﹣
﹣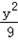 =1.
=1.

由
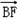 ,
,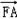 同向,
同向,∴渐近线的倾斜角为(0,
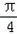 ),
),∴渐近线斜率为:

∴|AB|2=(|OB|﹣|OA|)(|OB|+|OA|)=(|OB|﹣|OA|)2|AB|,∴
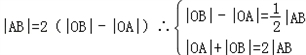
∴
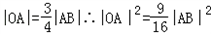
可得:
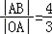 ,
,而在直角三角形OAB中,注意到三角形OAF也为直角三角形,即tan∠AOB=

而由对称性可知:OA的斜率为k=tan
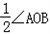
∴
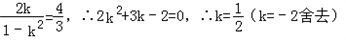 ;
;∴
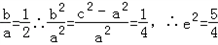 ∴
∴
(2)由第(1)知,a=2b,可设双曲线方程为
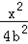 ﹣
﹣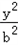 =1,c=
=1,c=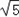 b,
b,∴AB的直线方程为 y=﹣2(x﹣
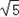 b),
b),代入双曲线方程得:15x2﹣32
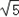 bx+84b2=0,
bx+84b2=0,∴x1+x2=
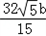 ,x1x2=
,x1x2=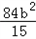 ,
,4=
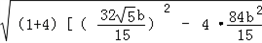 ,16=
,16=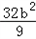 ﹣
﹣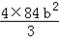 ,
,∴b2=9,所求双曲线方程为:
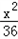 ﹣
﹣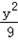 =1.
=1.
练习册系列答案
相关题目
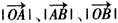 成等差数列,且
成等差数列,且 与
与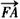 同向,
同向,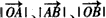 成等差数列,且
成等差数列,且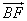 与
与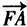 同向。
同向。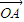 |、|
|、|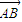 |、|
|、|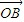 |成等差数列,且
|成等差数列,且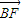 与
与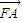 同向.
同向.