题目内容

函数y=1-2sin2x 是（　　）
分析：由二倍角公式可得，y=1-2sin2x=cos2x，可判断函数 的周期性及奇偶性
解答：解：由二倍角公式可得，y=1-2sin2x=cos2x
由周期公式可得，T=π，
∵f（-x）=cos（-2x）=cos2x=f（x）
∴函数为偶函数
故选B
点评：本题主要考查了二倍角公式在三角函数化简中的应用及函数的 周期性、奇偶性的判断，属于基础试题
练习册系列答案
相关题目
设函数y=1-2sin（
π
4
-x）cos（
π
4
-x），x∈R，则该函数是（　　）
下列命题中正确的是（　　）
（2012•三明模拟）（1）选修4-2：矩阵与变换
设矩阵M=
1a
b1
．
（I）若a=2，b=3，求矩阵M的逆矩阵M-1；
（II）若曲线C：x2+4xy+2y2=1在矩阵M的作用下变换成曲线C'：x2-2y2=1，求a+b的值．
（2）选修4-4：坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中x轴的正半轴重合．圆C的参数方程为
x=1+2cosα
y=-1+2sinα
（α为参数），点Q极坐标为(2，
7π
4
)．
（Ⅰ）化圆C的参数方程为极坐标方程；
（Ⅱ）若点P是圆C上的任意一点，求P、Q两点距离的最小值．
（3）选修4-5：不等式选讲
设函数f（x）=|x+1|+|x-2|．
（Ⅰ）求y=f（x）的最小值；
（Ⅱ）若关于x的不等式f（x）≥4的解集为A，求集合A．
设函数y=1-2sin（-x）cos（-x），x∈R，则该函数是（ ）
A．最小正周期为的奇函数
B．最小正周期为的偶函数
C．最小正周期为π的奇函数
D．最小正周期为π的偶函数
设函数y=1-2sin（
π
4
-x）cos（
π
4
-x），x∈R，则该函数是（　　）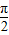
A．最小正周期为
π
2
的奇函数
B．最小正周期为
π
2
的偶函数
C．最小正周期为π的奇函数
D．最小正周期为π的偶函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网