题目内容
13.某经销商计划销售一款新型的空气净化器,经市场凋研发现以下规律:当每台净化器的利润为x(单位:元,x>0)时,销售量q(x)(单位:百台)与x的关系满足:若x不超过20,则q(x)=$\frac{1260}{x+1}$;若x大于或等于180,则销售为零;当20≤x≤180时.q(x)=a-b$\sqrt{x}$(a,b为实常数).(1)求函数q(x)的表达式;
(2)当x为多少时,总利润(单位:元)取得最大值,并求出该最大值.
分析 (1)分段函数由题意知分界点处函数值相等得到a,b
(2)总利润为每台的利润乘以销售量,分段函数每段求最大值,最后选择一个最大的为分段函数的最大值.
解答 解:(1)由x=20和x=180时可以解得a,b
$\left\{\begin{array}{l}{\frac{1260}{21}=a-b\sqrt{20}}\\{a-b\sqrt{180}=0}\end{array}\right.$
∴a=90,b=3$\sqrt{5}$
∴q(x)=$\left\{\begin{array}{l}{\frac{1260}{x+1}}&{0<x≤20}\\{90-3\sqrt{5x}}&{20≤x≤180}\\{0}&{x≥180}\end{array}\right.$
(2)设总利润为W(x)
则W(x)=$\left\{\begin{array}{l}{\frac{1260x}{x+1}}&{0<x≤20}\\{90x-3x\sqrt{5x}}&{20≤x≤180}\\{0}&{x≥180}\end{array}\right.$
①当x∈(0,20]时,W(x)=1260-$\frac{1260}{x+1}$为单调递增,最大值为1200,此时x=20
②当x∈[20,180]时,W(x)=90x-3x$\sqrt{5x}$,(W(x))′=90-$\frac{9\sqrt{5}}{2}\sqrt{x}$
此时x∈[20,80]时,W(x)单调递增.x∈[80,180]时,W(x)单调递减
∴在x=80时取得最大为2400
综上所述:x=80时,总利润最大为2400元.
点评 本题考查分段函数的解析式问题,由题意知分界点处函数值相等得到a,b.总利润为每台的利润乘以销售量,分段函数每段求最大值,最后选择一个最大的为分段函数的最大值.

| A. | f(x)=2sin$\frac{1}{2}$x | B. | f(x)=2cos2$\frac{1}{4}$x | C. | f(x)=2cos2$\frac{1}{2}$x | D. | f(x)=2cos$\frac{1}{2}$x |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{6}{7}$ | D. | $\frac{2}{21}$ |
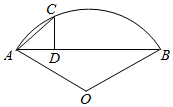 如图,若$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,C为劣弧AB上的一点,CD⊥AB于D,当点C在什么位置时,△ACD的面积最大,并求这个最大面积.
如图,若$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,C为劣弧AB上的一点,CD⊥AB于D,当点C在什么位置时,△ACD的面积最大,并求这个最大面积.