题目内容
5.已知数列{an}的各项均不为0,a1=$\frac{1}{2}$,且满足3an+1-an+2an+1an=0,数列{bn}满足bn=$\frac{1}{a_n}$+1.(Ⅰ)求证:数列{bn}为等比数列;
(Ⅱ)若cn=$\frac{n}{a_n}$,求数列{cn}的前n项和Sn.
分析 (Ⅰ)3an+1-an+2an+1an=0,an≠0,可得$\frac{1}{{a}_{n+1}}$=$\frac{3}{{a}_{n}}$+2,变形为:$\frac{1}{{a}_{n+1}}$+1=$3(\frac{1}{{a}_{n}}+1)$,bn+1=3bn.即可证明.
(Ⅱ)由(Ⅰ)知,bn=$\frac{1}{a_n}$+1=3n.可得an=$\frac{1}{{3}^{n}-1}$,cn=$\frac{n}{a_n}$=n×3n-n,再利用“错位相减法”、等差数列与等比数列的求和公式即可得出.
解答 (Ⅰ)证明:∵3an+1-an+2an+1an=0,an≠0,可得$\frac{1}{{a}_{n+1}}$=$\frac{3}{{a}_{n}}$+2,变形为:$\frac{1}{{a}_{n+1}}$+1=$3(\frac{1}{{a}_{n}}+1)$,
数列{bn}满足bn=$\frac{1}{a_n}$+1.∴bn+1=3bn.
∵a1=$\frac{1}{2}$,∴b1=3,
∴bn=$\frac{1}{a_n}$+1≠0.
∴数列{bn}是首项为3,公比为3的等比数列.…(4分)
(Ⅱ)解:由(Ⅰ)知,bn=$\frac{1}{a_n}$+1=3n.
∴an=$\frac{1}{{3}^{n}-1}$,…(5分)
∴cn=$\frac{n}{a_n}$=n×3n-n,…(7分)
∴Sn=1×3+2×32+…+n×3n-(1+2+…+n),…(8分)
设Tn=1×3+2×32+…+n×3n,①
∴3Tn=1×32+2×33+…+(n-1)×3n+n×3n+1,②
①-②得,-2Tn=3+32+…+3n-n×3n+1=$\frac{3({3}^{n}-1)}{3-1}$-n×3n+1=$\frac{(1-2n)×{3}^{n+1}}{2}$-$\frac{3}{2}$,
解得Tn=$\frac{(2n-1)•{3}^{n+1}}{4}$+$\frac{3}{4}$.
∴Sn=$\frac{(2n-1)•{3}^{n+1}}{4}$+$\frac{3}{4}$-$\frac{n(n+1)}{2}$.
点评 本题考查了“错位相减法”、等差数列与等比数列的定义通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.

| A. | (0,1] | B. | (0,2) | C. | $({0,\frac{3}{2}}]$ | D. | (0,2] |
| A. | 命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1” | |
| B. | 命题“若$?{x_0}∈R,{x_0}^2>1$”的否定是“?x∈R,x2<1” | |
| C. | 命题“若x=y,则cosx=cosy”的逆否命题为假命题 | |
| D. | 命题“若x=y,则cosx=cosy”的逆命题为假命题 |
| 男生 | 女生 | 合计 | |
| 收看 | 10 | ||
| 不收看 | 8 | ||
| 合计 | 30 |
(I)请将上面的列联表补充完整,并据此资料分析在犯错误概率不超过0.01的前提下“通过电视收看世界杯”与性别是否有关?
(II)若从这30名同学中的男同学中随机抽取2人参加一活动,记“通过电视收看世界杯”的人数为X,求X的分布列和均值.
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(c+a)(b+d)}$,n=a+b+c+d)
| P(K2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
| A. | (1,2) | B. | (2,1) | C. | (-1,2) | D. | (-2,-1) |
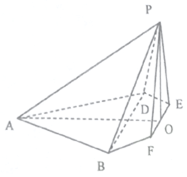 在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且$PB=\sqrt{10}$.
在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且$PB=\sqrt{10}$.