题目内容
在椭圆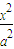 +
+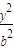 =1 (a>b>0)中,记左焦点为F,右顶点为A,短轴上方的端点为B.若该椭圆的离心率是
=1 (a>b>0)中,记左焦点为F,右顶点为A,短轴上方的端点为B.若该椭圆的离心率是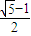 ,则∠ABF= .
,则∠ABF= .
【答案】分析:由题意得c=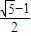 a,解出b2=a2-c2=
a,解出b2=a2-c2=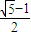 a2.在△ABF中分别计算出|AB|2、|BF|2和|AF|2,可得AF|2=|AB|2+|BF|2,所以△ABF是以AF为斜边的直角三角形,即∠ABF=90°.
a2.在△ABF中分别计算出|AB|2、|BF|2和|AF|2,可得AF|2=|AB|2+|BF|2,所以△ABF是以AF为斜边的直角三角形,即∠ABF=90°.
解答: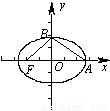 解:∵椭圆的离心率是
解:∵椭圆的离心率是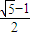 ,
,
∴c=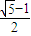 a,可得|AF|=c+a=(
a,可得|AF|=c+a=(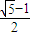 +1)a=
+1)a=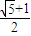 a.
a.
而b2=a2-c2=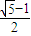 a2,
a2,
∴|AB|2=|AO|2+|OB|2=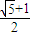 a2.
a2.
因为|BF|=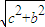 =a,
=a,
所以|AB|2+|BF|2=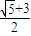 a2
a2
∵|AF|2=(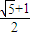 a)2=
a)2= a2
a2
∴|AF|2=|AB|2+|BF|2.得△ABF是以AF为斜边的直角三角形,即∠ABF=90°.
故答案为:90°.
点评:本题给出特殊离心率的椭圆,求椭圆的上顶点对左焦点、右顶点的张角,着重考查了椭圆的标准方程和简单性质、直角三角形的判定等知识,属于基础题.
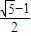 a,解出b2=a2-c2=
a,解出b2=a2-c2=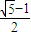 a2.在△ABF中分别计算出|AB|2、|BF|2和|AF|2,可得AF|2=|AB|2+|BF|2,所以△ABF是以AF为斜边的直角三角形,即∠ABF=90°.
a2.在△ABF中分别计算出|AB|2、|BF|2和|AF|2,可得AF|2=|AB|2+|BF|2,所以△ABF是以AF为斜边的直角三角形,即∠ABF=90°.解答:
 解:∵椭圆的离心率是
解:∵椭圆的离心率是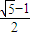 ,
,∴c=
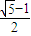 a,可得|AF|=c+a=(
a,可得|AF|=c+a=(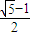 +1)a=
+1)a=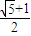 a.
a.而b2=a2-c2=
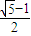 a2,
a2,∴|AB|2=|AO|2+|OB|2=
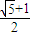 a2.
a2.因为|BF|=
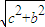 =a,
=a,所以|AB|2+|BF|2=
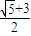 a2
a2∵|AF|2=(
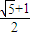 a)2=
a)2= a2
a2∴|AF|2=|AB|2+|BF|2.得△ABF是以AF为斜边的直角三角形,即∠ABF=90°.
故答案为:90°.
点评:本题给出特殊离心率的椭圆,求椭圆的上顶点对左焦点、右顶点的张角,着重考查了椭圆的标准方程和简单性质、直角三角形的判定等知识,属于基础题.

练习册系列答案
相关题目

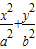 =1(a>b>0)的左准线上.过点P且方向为
=1(a>b>0)的左准线上.过点P且方向为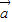 =(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( )
=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( )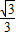

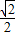

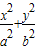 =1(a>b>0)的左准线上.过点P且方向为
=1(a>b>0)的左准线上.过点P且方向为 =(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( )
=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( )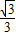

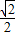

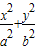 =1(a>b>0)上,AB∥x轴,AD过左焦点F,则该椭圆的离心率为 .
=1(a>b>0)上,AB∥x轴,AD过左焦点F,则该椭圆的离心率为 . =1(a>b>0)上,AB∥x轴,AD过左焦点F,则该椭圆的离心率为 .
=1(a>b>0)上,AB∥x轴,AD过左焦点F,则该椭圆的离心率为 .