题目内容

已知正方形ABCD的四个顶点在椭圆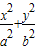=1（a＞b＞0）上，AB∥x轴，AD过左焦点F，则该椭圆的离心率为    ．
【答案】分析：由于正方形ABCD的四个顶点在椭圆=1（a＞b＞0）上，AB∥x轴，AD过左焦点F，所以点在椭圆上，代入椭圆方程即可求离心率．
解答：解：根据题意，点在椭圆上，
故有，∴，
故答案为．
点评：本题主要考查了椭圆的简单性质和椭圆的标准方程．考查了学生对椭圆基础知识的掌握和灵活运用．
练习册系列答案
相关题目
已知正方形ABCD的边长为2，中心为O，四边形PACE是直角梯形，设PA⊥平面ABCD，且PA=2，CE=1，
（1）求证：面PAD∥面BCE．
（2）求PO与平面PAD所成角的正弦．
（3）求二面角P-EB-C的正切值．
如图，已知正方形ABCD的中心为E（-1，0），一边AB所在的直线方程为x+3y-5=0，求其它三边所在的直线方程．
已知正方形ABCD的边长是4，对角线AC与BD交于O，将正方形ABCD沿对角线BD折成60°的二面角，并给出下面结论：①AC⊥BD；②AD⊥CO；③△AOC为正三角形；④cos∠ADC=
3
4
，则其中的真命题是（　　）
已知正方形ABCD的边长为1，设
AB
=
a
，
BC
=
b
，
AC
=
c
，则|
a
-
b
+
c
|等于（　　）
A、0
B、
2
C、2
D、2
2
已知正方形ABCD的边长为
2
，
AB
=
a
，
BC
=
b
，
AC
=
c
，则|
a
+
b
+
c
|=
4
4
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网