题目内容
（本题满分12分）在直角坐标平面中，△
的两个顶点
的坐标分别为
，
，平面内两点
同时满足下列条件：①
=0；②
；③
∥
（1）求△的顶点
的轨迹方程；（2）过点
直线
与（1）中轨迹交于不同的两点
，求△
面积的最大值.
(Ⅰ) 
(Ⅱ) 
解析:
（1）设
∵
∴M点在线段AB的中垂线上.由已知A(－1，0)，B(1,0)，∴xM=0.
∴(－1－x0，－y0)+（1－x0,－y0）+(x－x0，y－y0)=(0,0),∴x0=
，y0=
，∴
∵
，∴
∴
∴顶点C的轨迹方程为
（4分）
（2）设直线l方程为: 
，E(x1，y1)，F(x2,y2)，
由
，消去y得：
①
∴
（6分）
∴
，
-----10分
设
，则
在
单调递减。
故当
，即
时，
----12分
练习册系列答案
相关题目
．
，求△ABC的面积．
，0），若实数λ使向量
，λ
，
满足λ2·（
时，过点A1且斜率为1的直线与此时（1）中的曲线相交的另一点为B，能否在直线x=-9上找一点C，使ΔA1BC为正三角形（请说明理由）。
中
分别为A,B,C所对的边，
且
，求
的取值范围
中，数列的前n项和
满足
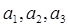；（2） 由（1）猜想数列
中，E是BC的中点，F是
的中点
的平面角的余弦值。