题目内容
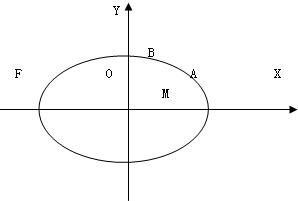如图所示，椭圆过点B(0，| 5 |
| AF |
| FM |
| 1 |
| 2 |
| FO |
（1）求椭圆的方程．
（2）若动点P（x，y），符合条件：
| PM |
| PA |
分析：（1）先根据题意确定b=
，再由
=
可以得到a=
c，最后根据椭圆的基本性质a2=b2+c2可以求出a，b，c的值，从而确定椭圆方程．
（2）先求出点F，M，A的坐标，根据P满足条件
•
=0可得到p轨迹方程，然后与椭圆方程联立发现仅有一个公共点A（3，0），又因为当y≠0时考虑，故要舍弃，从而得证．
| 5 |
| AF |
| 1 |
| 2 |
| FO |
| 3 |
| 2 |
（2）先求出点F，M，A的坐标，根据P满足条件
| PM |
| PA |
解答：解：（1）依题意得：b=
∵
=
，
∴2（a-c）=c，
∴a=
c
∵a2=b2+c2，∴c=2
∴a=3，c=2，b=
，
故椭圆的方程
+
=1．
（2）由动点P（x，y）符合条件
•
=0，F（2，0）、M（1，0）、A（3，0）
得P（x，y）的轨迹方程：（x-2）2+y2=1，是以F（2，0）为圆心，1为半径的圆．
联立椭圆的方程
+
=1得：公共点仅为A（3，0）
又y≠0所以A（3，0）舍去，从而该圆始终在椭圆内部．
故动点P（x，y）一定在椭圆内部．
| 5 |
∵
| AF |
| 1 |
| 2 |
| FO |
∴2（a-c）=c，
∴a=
| 3 |
| 2 |
∵a2=b2+c2，∴c=2
∴a=3，c=2，b=
| 5 |
故椭圆的方程
| x2 |
| 9 |
| y2 |
| 5 |
（2）由动点P（x，y）符合条件
| PM |
| PA |
得P（x，y）的轨迹方程：（x-2）2+y2=1，是以F（2，0）为圆心，1为半径的圆．
联立椭圆的方程
| x2 |
| 9 |
| y2 |
| 5 |
又y≠0所以A（3，0）舍去，从而该圆始终在椭圆内部．
故动点P（x，y）一定在椭圆内部．
点评：本题主要考查椭圆的基本性质和动点的轨迹方程．椭圆在圆锥曲线中占据重要的位置，在高考中所占的比重特别大，一定要强化复习．
练习册系列答案
相关题目
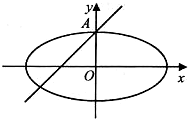如图所示，椭圆
如图所示，椭圆C：
(a＞b＞0)的右焦点为F(c，0)，过点F的一动直线m绕点F转动，并且交椭圆于A、B两点，P为线段AB的中点．
，
．确定θ的值，使原点距椭圆Q的右准线l最远．此时，设l与x轴交点为D，当直线m绕点F转动到什么位置时，△ABD的面积最大?
，点
、
分别为椭圆的右焦点和右顶点
且有
，符合条件：
，当
时，求证：动点
