题目内容
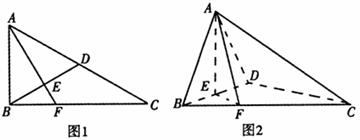
如图1,在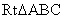 中,
中,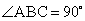 ,
,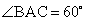 ,
, ,
, 、
、 分别为
分别为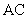 、
、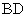 的中点,连接
的中点,连接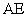 并延长交
并延长交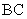 于
于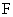 ,将
,将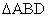 沿
沿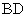 折起,使平面
折起,使平面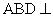 平面
平面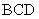 ,如图2所示.
,如图2所示.
 求证:
求证: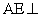 平面
平面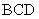 ;
;
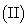 求平面
求平面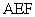 与平面
与平面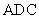 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
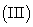 在线段
在线段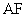 上是否存在点
上是否存在点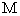 使得
使得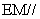 平面
平面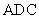 ?若存在,请指出点
?若存在,请指出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
 |
(1)在 中,
中, 为AC的中点,
为AC的中点, 又
又 ,所以三角形
,所以三角形 为等边三角形;
为等边三角形; 为BD的中点,
为BD的中点, 于E,因为平面
于E,因为平面 平面
平面 ,交线为BD,
,交线为BD, 平面
平面 ,所以
,所以 平面
平面 ;
;
(2)由(1)结论知: 平面
平面 ,
, ,由题意知
,由题意知 ,以
,以 为坐标原点,分别以
为坐标原点,分别以 所在直线为
所在直线为 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系
轴,建立空间直角坐标系 ,由(1)得,
,由(1)得,
计算:
则 ,
, ,则
,则

 ,易知平面
,易知平面 的一个法向量为
的一个法向量为 ,
,
设平面 的法向量为
的法向量为 ,则
,则
 ,即
,即 ,
,
令
 .
.
 .
.
所以平面 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为
(3)设 ,其中
,其中 ,
,
 ,其中
,其中 ,
, ,由
,由 解得
解得 .
.
所以在线段 上存在点
上存在点 ,使
,使 平面
平面 ,且
,且 :
: :
: .
.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 .
. ,求
,求 五个数字中每次取出三个不同的数字组成三位数,
五个数字中每次取出三个不同的数字组成三位数, 位偶数
位偶数
 在区间
在区间 内为减函数,在区间
内为减函数,在区间 为增函数,则实数
为增函数,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C.  D.
D.  .
. ,则
,则 ( )
( ) D.1
D.1 上单调递增的函数是( )
上单调递增的函数是( ) B.
B. C.
C. D.
D.