题目内容
已知函数
．
（1）求m的值；
（2）当a＞1，x∈（r，a-2）时f（x）的值域是（1，+∞），求实数a与r的值．
解：（1）由函数f（x）是奇函数可得：
=-
；
解得m=-1；
∵
，∴
，∴
，
∴
分析：（1）根据f（-x）=-f（x）得到m的值即可；
（2）由a＞1时f（x）＞1得
，解出x的取值范围，又因为x∈（r，a-2），所以得r=1，a-2=
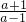，a＞1，解出a的值即可．
点评：考查学生运用函数奇偶性的能力，以及对数函数的值域与最值的掌握能力．
=-；解得m=-1；
∵
，∴，∴，∴
分析：（1）根据f（-x）=-f（x）得到m的值即可；
（2）由a＞1时f（x）＞1得
，解出x的取值范围，又因为x∈（r，a-2），所以得r=1，a-2=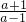，a＞1，解出a的值即可．点评：考查学生运用函数奇偶性的能力，以及对数函数的值域与最值的掌握能力．
练习册系列答案
阅读快车系列答案
相关题目
。
上的单调性并加以证明；
的值域是（1，+
），求a的值。
。
上的单调性并加以证明；
的值域是（1，+
），求a的值。