题目内容
 如图所示,设曲线y=
如图所示,设曲线y=| 1 |
| x |
| 1 |
| x |
(1)求a1,并求出an和an-1 n∈N*之间的关系式;
(2)求数列{an}的通项公式;
(3)设bn=
| 2 |
| an-1+an |
分析:(1)由题设知a1=
+
,由此能求出a1,利用△An-1BnAn为等腰直角三角形,且Bn为直角顶点,求出Bn点的横纵坐标,再根据Bn点为函数y=
(x>0)图象上的点,坐标满足函数y=
(x>0)的解析式,就可得到an和an-1 之间的关系式.
(2)由(1)知数列{an2}是首项为4,公差为4的等差数列,由此能求出数列{an}的通项公式.
(3)由bn=
=
=
-
,能求出数列{bn}的前n项和Sn.
| a1 |
| 2 |
| 2 |
| a1 |
| 1 |
| x |
| 1 |
| x |
(2)由(1)知数列{an2}是首项为4,公差为4的等差数列,由此能求出数列{an}的通项公式.
(3)由bn=
| 2 |
| an-1+an |
| 1 | ||||
|
| n |
| n-1 |
解答:解:(1)∵曲线y=
上的点与x轴上的点顺次构成等腰直角三角形△OB1A1,△A1B2A2,…,直角顶点在曲线上y=
,设An的坐标为(an,0),A0为原点,
∴a1=
+
,
解得a1=2.
过Bn点作BnH⊥x轴,垂足为H,
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴|BnH|=
|An-1An|=
,
∴Bn点的纵坐标为
,
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴H点为线段An-1An的中点,
∴H点横坐标为
,
∵BnH⊥x轴,∴Bn点的横坐标也为
,
∵Bn点为函数y=
(x>0)图象上的点,
∴
•
=1
∴an2-an-12=4.
(2)∵an2-an-12=4,a1=2,
∴数列{an2}是首项为4,公差为4的等差数列,
∴an2=4n,
∴an=2
.
(3)∵bn=
=
=
-
,
∴Sn=(
-
)+(
-
)+…+(
-
)
=
.
| 1 |
| x |
| 1 |
| x |
∴a1=
| a1 |
| 2 |
| 2 |
| a1 |
解得a1=2.
过Bn点作BnH⊥x轴,垂足为H,
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴|BnH|=
| 1 |
| 2 |
| an-an-1 |
| 2 |
∴Bn点的纵坐标为
| an-an-1 |
| 2 |
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴H点为线段An-1An的中点,
∴H点横坐标为
| an+an-1 |
| 2 |
∵BnH⊥x轴,∴Bn点的横坐标也为
| an+an-1 |
| 2 |
∵Bn点为函数y=
| 1 |
| 2 |
∴
| an-an-1 |
| 2 |
| an+an-1 |
| 2 |
∴an2-an-12=4.
(2)∵an2-an-12=4,a1=2,
∴数列{an2}是首项为4,公差为4的等差数列,
∴an2=4n,
∴an=2
| n |
(3)∵bn=
| 2 |
| an-1+an |
=
| 1 | ||||
|
=
| n |
| n-1 |
∴Sn=(
| 1 |
| 0 |
| 2 |
| 1 |
| n |
| n-1 |
=
| n |
点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,仔细解答,注意数与函数的综合应用.

练习册系列答案
相关题目
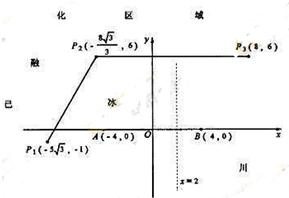
 为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(如图).考察范围到A、B两点的距离之和不超过10Km的区域.
为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(如图).考察范围到A、B两点的距离之和不超过10Km的区域. (2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
(2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.