题目内容
设AB为过椭圆b2x2+a2y2=a2b2中心的弦,F1为焦点,求△F1AB的最大面积.解:如图,△F1AB的面积是平行四边形F1AF2B的面积之半,且等于△AF1F2面积,只有A点位于短轴端点时,△AF1F2的面积才能达到最大值,从而得解.

设椭圆的另一焦点为F2,因O是AB、F1F2的中点,故四边形F1AF2B为平行四边形.∴△F1AB与△AF1F2的面积相等.
设点A坐标为(x1,y1),则△AF1F2的面积可得,即
![]() =
=![]() |F1F2|·|y1|.由b2x12+a2y12=a2b2得y12=
|F1F2|·|y1|.由b2x12+a2y12=a2b2得y12=![]() (a2-x12). ∴|y1|=
(a2-x12). ∴|y1|=![]()
![]() .
.
当x1=0时,|y1|取得最大值b,∴△AF1F2的最大面积为![]() ·2c·b=bc.
·2c·b=bc.
即(![]() )max=bc.
)max=bc.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
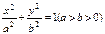 的离心率为
的离心率为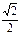 .
.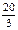 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程; 的值.
的值.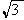 y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求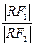 的值.
的值.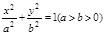 的离心率为
的离心率为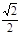 .
.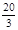 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;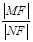 的值.
的值.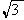 y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求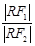 的值.
的值.