题目内容
已知椭圆
+
=1(b>0)
(1)若圆(x-2)2+(y-1)2=
(2)与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆方程;
(3)设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为60°.求
的值.
| x2 |
| 2b2 |
| y2 |
| b2 |
(1)若圆(x-2)2+(y-1)2=
| 20 |
| 3 |
(2)与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆方程;
(3)设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为60°.求
| |MF| |
| |NF| |
分析:(1)由于AB为圆的直径,即A、B两点之间的距离为圆的半径,故可设直线方程代入椭圆方程.利用中点坐标及弦长公式可求椭圆的方程;
(2)由于L的倾斜角为60°,利用椭圆的第二定义,可建立方程,从而可求比值
(2)由于L的倾斜角为60°,利用椭圆的第二定义,可建立方程,从而可求比值
解答:解:(1)设A(x1,y1),B(x2,y2),AB的方程为y-1=k(x-2)即y=kx+1-2k
代入
+
=1(b>0)得(1+2k2)x2+4(1-2k)•kx+2(1-2k)2-2b2=0
∵x1+x2=
=4∴k=-1
∴x1x2=6-
b2∴(x1-x2)2=
∴b2=8∴椭圆方程为
+
=1;
(2)设 MF=m,NF=n(不妨设m<n)则由第二定义知
-
=
(m+n)
即
=
或
=
∴
=
或
=
.
代入
| x2 |
| 2b2 |
| y2 |
| b2 |
∵x1+x2=
| 4(1-2k)k |
| 1+2k2 |
∴x1x2=6-
| 2 |
| 3 |
| 40 |
| 3 |
∴b2=8∴椭圆方程为
| x2 |
| 16 |
| y2 |
| 8 |
(2)设 MF=m,NF=n(不妨设m<n)则由第二定义知
| n |
| e |
| m |
| e |
| 1 |
| 2 |
即
| m |
| n |
9+4
| ||
| 7 |
| m |
| n |
9-4
| ||
| 7 |
∴
| |MF| |
| |NF| |
9+4
| ||
| 7 |
| |MF| |
| |NF| |
9-4
| ||
| 7 |
点评:本题以椭圆为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,有较强的综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
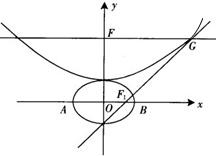 设b>0,椭圆方程为
设b>0,椭圆方程为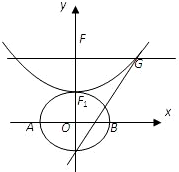 设b>0,椭圆方程为
设b>0,椭圆方程为