题目内容
(本题满分16分)已知椭圆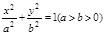 的离心率为
的离心率为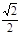 .
.
⑴若圆(x-2)2+(y-1)2=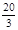 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
⑵设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为600.求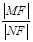 的值.
的值.
⑶在(1)的条件下,椭圆W的左右焦点分别为F1、 F2,点R在直线l:x-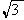 y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求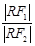 的值.
的值.
【答案】
解:(1)设A(x1,y1),B(x2,y2),AB的方程为y-1=k(x-2) 即y=kx+1-2k①
∵离心率e=
∴椭圆方程可化为 ②
②
将①代入②得(1+2k2)x2+4(1-2k)·kx
+2(1-2k)2-2b2=0
∵x1+x2= ∴k=-1
∴k=-1
∴x1x2=
又
∴ 即
即
∴b2=8
∴椭圆方程为
(2)设 ,则由第二定义知
,则由第二定义知 即
即 或
或
∴ 或
或 .
.
(3)当∠F1RF2取最大值时,过R、F1、F2的圆的圆心角最大,故其半径最小,与直线l相切.
直线l与x轴于S(-8,0), ∽
∽ (可证)
(可证)

【解析】略

练习册系列答案
相关题目
 ,且对任意
,且对任意 ,有
,有 .
. ;
; 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数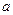 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
) 为实常数).
为实常数). 时,求函数
时,求函数 在
在 上的最小值;
上的最小值; 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
 )
) :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值. 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 。
。 及
及 的值;
的值; 上的解析式;
上的解析式; 的方程
的方程 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围。
的取值范围。