题目内容
设点 、
、 分别是椭圆
分别是椭圆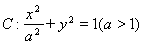 的左、右焦点,
的左、右焦点, 为椭圆
为椭圆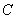 上任意一点,且
上任意一点,且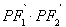 的最小值为
的最小值为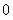 .
.
(I)求椭圆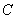 的方程;
的方程;
(II)设直线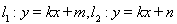 (直线
(直线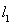 、
、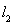 不重合),若
不重合),若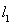 、
、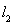 均与椭圆
均与椭圆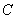 相切,试探究在
相切,试探究在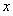 轴上是否存在定点
轴上是否存在定点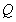 ,使点
,使点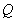 到
到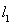 、
、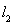 的距离之积恒为1?若存在,请求出点
的距离之积恒为1?若存在,请求出点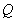 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
【答案】
(1) ;(2)定点
;(2)定点 存在,其坐标为
存在,其坐标为 或
或 .
.
【解析】
试题分析:本题考查椭圆的标准方程以及直线与椭圆的位置关系等数学知识,考查分析问题解决问题的能力和计算能力,考查函数思想和分类讨论思想.第一问,设出 点坐标,用代数法解题,得到向量
点坐标,用代数法解题,得到向量 和
和 的坐标,利用向量的数量积得出表达式,求出最小值,即可解出
的坐标,利用向量的数量积得出表达式,求出最小值,即可解出 的值,即确定了
的值,即确定了 的值,写出椭圆的方程;第二问,由于直线与椭圆相切,所以直线与椭圆方程联立消参,得出方程的判别式等于0,得出
的值,写出椭圆的方程;第二问,由于直线与椭圆相切,所以直线与椭圆方程联立消参,得出方程的判别式等于0,得出 ,同理,得出
,同理,得出 ,所以
,所以 ,因为两直线不重合,所以
,因为两直线不重合,所以 ,若存在点
,若存在点 ,利用点到直线的距离公式得到距离之积为1的表达式,解出
,利用点到直线的距离公式得到距离之积为1的表达式,解出 的值,由于
的值,由于 的值存在,所以存在点
的值存在,所以存在点 ,写出坐标即可.
,写出坐标即可.
试题解析:(I)设 ,则有
,则有 ,
,

由 最小值为
最小值为 得
得 ,
,
∴椭圆 的方程为
的方程为 4分
4分
(II)把 的方程代入椭圆方程得
的方程代入椭圆方程得
∵直线 与椭圆
与椭圆 相切,∴
相切,∴ ,化简得
,化简得
同理可得:
∴ ,若
,若 ,则
,则 重合,不合题意,
重合,不合题意,
∴ ,即
,即 8分
8分
设在 轴上存在点
轴上存在点 ,点
,点 到直线
到直线 的距离之积为1,则
的距离之积为1,则
 ,即
,即 ,
,
把 代入并去绝对值整理,
代入并去绝对值整理, 或者
或者
前式显然不恒成立;而要使得后式对任意的 恒成立
恒成立
则 ,解得
,解得 ;
;
综上所述,满足题意的定点 存在,其坐标为
存在,其坐标为 或
或 . 12分
. 12分
考点:1.椭圆的标准方程;2.向量的数量积;3.点到直线的距离公式.

练习册系列答案
相关题目
 、
、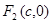 分别是椭圆
分别是椭圆 的左、右焦点,
的左、右焦点, 为椭圆
为椭圆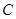 上任意一点,且
上任意一点,且 最小值为
最小值为 .
.
 均与椭圆
均与椭圆 ,试探究在
,试探究在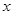 轴上是否存在定点
轴上是否存在定点 ,点
,点