题目内容
数列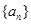 中,
中,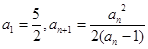
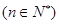 ,用数学归纳法证明:
,用数学归纳法证明: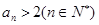 。
。
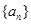 中,
中,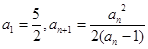
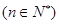 ,用数学归纳法证明:
,用数学归纳法证明: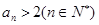 。
。对于关于自然数的的命题可知通过数学归纳法来加以证明。分为两个步骤,第一步,证明n取第一个值成立,假设n=k成立来推理得到n=k+1成立。
试题分析:
解:(1) 当n=1时,
 ,不等式成立.
,不等式成立.(2)假设当n=k时不等式成立,即
 ,
,则

 ,
,
 当n=k+1时, 不等式也成立
当n=k+1时, 不等式也成立综合(1)(2),不等式对所有正整数都成立
点评:主要是考查了数学归纳法来证明不等式的运用,属于基础题。

练习册系列答案
相关题目

 是等差数列,
是等差数列, ,数列
,数列 的前n项和是
的前n项和是 ,且
,且 .
. .
.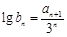 ,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由. ,求n的值;
,求n的值; 的数学公式表示上述结论,并给予证明。
的数学公式表示上述结论,并给予证明。
 中,有
中,有 ,则此数列的前13项之和为 .
,则此数列的前13项之和为 .  的前三项依次为
的前三项依次为 ,
, ,
, ,则此数列的通项公式为( )
,则此数列的通项公式为( )



 前
前 项和
项和 ,
, ,则公差d的值为 ( )
,则公差d的值为 ( )