题目内容
13. 设平行于y轴的直线分别与函数y1=log2x及y2=log2x+2的图象交于B,C两点,点A(m,n)位于函数y2的图象上,若△ABC为正三角形,则m•2n=( )
设平行于y轴的直线分别与函数y1=log2x及y2=log2x+2的图象交于B,C两点,点A(m,n)位于函数y2的图象上,若△ABC为正三角形,则m•2n=( )| A. | 8$\sqrt{3}$ | B. | 12 | C. | 12$\sqrt{3}$ | D. | 15 |
分析 根据题意,设出A、B、C的坐标,由线段BC∥y轴,△ABC是等边三角形,得出AB、AC与BC的关系,求出p、q的值,计算出结果
解答 解:根据题意,设A(m,n),B(x0,log2x0),C(x0,2+log2x0),
∵线段BC∥y轴,△ABC是等边三角形,
∴BC=2,2+log2m=n,
∴m=2n-2,
∴4m=2n;
又x0-m=$\sqrt{3}$,
∴m=x0-$\sqrt{3}$,
∴x0=m+$\sqrt{3}$;
又2+log2x0-n=1,
∴log2x0=n-1,x0=2n-1=$\frac{{2}^{n}}{2}$;
∴m+$\sqrt{3}$=$\frac{{2}^{n}}{2}$;2m+2$\sqrt{3}$=2n=4m,
∴m=$\sqrt{3}$,2n=4$\sqrt{3}$;
∴m•2n=$\sqrt{3}$×4$\sqrt{3}$=12;
故选:B
点评 本题考查了指数函数与对数函数的图象与性质的应用问题,也考查了指数,对数的运算问题,是较难的题目.

练习册系列答案
相关题目
4.“a=1“是“直线ax+y+1=0与直线(a+2)x-3y-2=0垂直”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
1. 如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )
如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )
 如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )
如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )| A. | k<132? | B. | k<70? | C. | k<64? | D. | k<63? |
18.已知F为抛物线C:y2=4x的焦点,点E在C的准线上,且在x轴上方,线段EF的垂直平分线与C的准线交于点Q(-1,$\frac{3}{2}$),与C交于点P,则点P的坐标为( )
| A. | (1,2) | B. | (2,2$\sqrt{2}$) | C. | (3,2$\sqrt{3}$) | D. | (4,4) |
3.在边长为2的正方形ABCD中,E,F分别为BC和DC的中点,则$\overrightarrow{DE}$•$\overrightarrow{BF}$=( )


| A. | -$\frac{5}{2}$ | B. | $\frac{3}{2}$ | C. | -4 | D. | -2 |
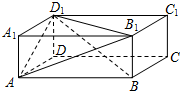 如图,在长方体ABCD-A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1-ABD1的体积为1cm3.
如图,在长方体ABCD-A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1-ABD1的体积为1cm3. 如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC,AB=BC=CA=$\frac{1}{2}A{A_1}$=1,∠A1AB=120°,D、E分别是BC、A1C1的中点.
如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC,AB=BC=CA=$\frac{1}{2}A{A_1}$=1,∠A1AB=120°,D、E分别是BC、A1C1的中点.