题目内容
9．在空间直角坐标系中，已知A（1，0，2），B（1，-3，1），在z轴上存在点M，使得|MA|=|MB|，则M点的坐标为（ ）| A． | （0，0，3） | B． | （0，0，-3） | C． | （0，0，-6） | D． | （0，0，6） |
分析 设出点M（0，0，z），由|MA|=|MB|，建立关于参数z的方程，求y值即可．
解答 解：设设M（0，0，z），由|MA|=|MB|，
可得$\sqrt{1+（2-z）^{2}}$=$\sqrt{1+9+（1-z）^{2}}$，即（2-z）2+1=（1-z）2+10，解得：z=-3．
M的坐标是（0，0，-3）．
故选：B．
点评 本题考点是点、线、面间的距离计算，空间两点距离公式的应用，考查计算能力．
练习册系列答案
相关题目
20．设D是△ABC所在平面内一点，$\overrightarrow{AB}$=-2$\overrightarrow{DC}$，则（ ）
| A． | $\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ | B． | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{3}{2}$$\overrightarrow{AB}$ | C． | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{1}{2}$$\overrightarrow{AB}$ | D． | $\overrightarrow{BD}$=$\frac{3}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ |
14．执行如图程序框图，如果输入的N的值是6，那么输出的p的值是（ ）
| A． | 105 | B． | 115 | C． | 120 | D． | 720 |
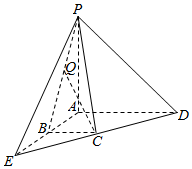如图，PA⊥平面ADE，B，C分别是AE，DE的中点，AE⊥AD，AD=AE=AP=2．
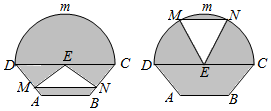如图所示的是自动通风设施．该设施的下部ABCD是等腰梯形，其中AB=1米，高0.5米，CD=2米．上部CmD是个半圆，固定点E为CD的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆．