МвДҝДЪИЭ
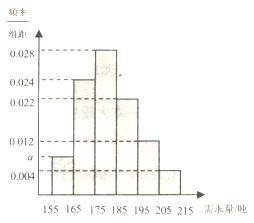
ЎҫМвДҝЎҝОӘБЛҪвРЎС§ЙъөДМеДЬЗйҝцЈ¬ПЦійИЎДіРЎС§БщДкј¶100ГыС§ЙъҪшРРМшЙюІвКФЈ¬№ЫІмјЗВјәўЧУГЗИэ·ЦЦУДЪөДМшЙюёцКэЈ¬Ҫ«ЛщөГөДКэҫЭХыАнәу»ӯіцЖөВК·ЦІјЦұ·ҪНјЈ¬МшЙюёцКэөДКэЦөВдФЪЗшјд![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ДЪөДЖөВКЦ®ұИОӘ
ДЪөДЖөВКЦ®ұИОӘ![]() .ЈЁјЖЛгҪб№ыұЈБфРЎКэөгәуГж3О»Ј©
.ЈЁјЖЛгҪб№ыұЈБфРЎКэөгәуГж3О»Ј©

ЈЁўсЈ©ЗуХвЩѧЙъМшЙюёцКэөДКэЦөВдФЪЗшјд![]() ДЪөДЖөВКЈ»
ДЪөДЖөВКЈ»
ЈЁўтЈ©УГ·ЦІгійСщөД·Ҫ·ЁФЪЗшјд![]() ДЪійИЎТ»ёцИЭБҝОӘ6өДСщұҫЈ¬Ҫ«ёГСщұҫҝҙіЙТ»ёцЧЬМеЈ¬ҙУЦРИОТвСЎИЎ2ёцС§ЙъЈ¬ЗуХв2ёцС§ЙъМшЙюёцКэөДКэЦө¶јФЪЗшјд
ДЪійИЎТ»ёцИЭБҝОӘ6өДСщұҫЈ¬Ҫ«ёГСщұҫҝҙіЙТ»ёцЧЬМеЈ¬ҙУЦРИОТвСЎИЎ2ёцС§ЙъЈ¬ЗуХв2ёцС§ЙъМшЙюёцКэөДКэЦө¶јФЪЗшјд![]() ДЪөДёЕВК.
ДЪөДёЕВК.
Ўҫҙр°ёЎҝЈЁўсЈ©0.05Ј»ЈЁўтЈ©![]() .
.
ЎҫҪвОцЎҝ
ЈЁўсЈ©ёщҫЭЖөВКЦ®ұИЈ¬ҝЙјЩЙиКэЦөВдФЪЗшјд![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() өДЖөВКЈ¬И»әуАыУГЛщУРЖөВКЦ®әНОӘ1Ј¬ҝЙөГҪб№ы.
өДЖөВКЈ¬И»әуАыУГЛщУРЖөВКЦ®әНОӘ1Ј¬ҝЙөГҪб№ы.
ЈЁўтЈ©ёщҫЭЗшјд![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ДЪөДЖөВКЦ®ұИОӘЈә3Јә2Јә1Ј¬°ҙ·ЦІгійСщөД·Ҫ·ЁҪ«ХвИэёцЗшјдөДЛщійИЎөДИЛКэ·ЦұрҪшРРұкәЕЈ¬ІЙУГБРҫЩ·ЁЈ¬И»әуАыУГ№ЕөдёЕРНЈ¬ҝЙөГҪб№ы.
ДЪөДЖөВКЦ®ұИОӘЈә3Јә2Јә1Ј¬°ҙ·ЦІгійСщөД·Ҫ·ЁҪ«ХвИэёцЗшјдөДЛщійИЎөДИЛКэ·ЦұрҪшРРұкәЕЈ¬ІЙУГБРҫЩ·ЁЈ¬И»әуАыУГ№ЕөдёЕРНЈ¬ҝЙөГҪб№ы.
ЈЁўсЈ©ЙиЗшјд![]() ДЪөДЖөВКОӘ
ДЪөДЖөВКОӘ![]() Ј¬ФтЗшјд
Ј¬ФтЗшјд![]() Ј¬
Ј¬![]() ДЪөДЖөВК·ЦұрОӘ
ДЪөДЖөВК·ЦұрОӘ![]() әН
әН![]() Ј¬ТАМвТвөГЈә
Ј¬ТАМвТвөГЈә ![]() .ҪвөГ
.ҪвөГ![]() .
.
ЛщТФЗшјд![]() ДЪөДЖөВКОӘ0.05.
ДЪөДЖөВКОӘ0.05.
ЈЁўтЈ©УЙЈЁўсЈ©өГЈәЗшјд![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ДЪөДЖөВКТАҙООӘ0.3Ј¬0.2Ј¬0.1.
ДЪөДЖөВКТАҙООӘ0.3Ј¬0.2Ј¬0.1.
УГ·ЦІгійСщөД·Ҫ·ЁФЪЗшјд![]() ДЪійИЎТ»ёцИЭБҝОӘ6өДСщұҫ.
ДЪійИЎТ»ёцИЭБҝОӘ6өДСщұҫ.
ФтФЪЗшјд![]() ДЪУҰійИЎ
ДЪУҰійИЎ![]() ИЛЈ¬јЗОӘ
ИЛЈ¬јЗОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
ФЪЗшјд![]() ДЪУҰійИЎ
ДЪУҰійИЎ![]() ИЛЈ¬јЗОӘ
ИЛЈ¬јЗОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ФЪЗшјд![]() ДЪУҰійИЎ
ДЪУҰійИЎ![]() ИЛЈ¬јЗОӘ
ИЛЈ¬јЗОӘ![]() .
.
ЙиЎ°ҙУЦРИОТвСЎИЎ2ёцәўЧУЈ¬Хв2ёцәўЧУМшЙюКэЦө¶јФЪЗшјд![]() ДЪЎұОӘКВјю
ДЪЎұОӘКВјю![]() Ј¬
Ј¬
ФтЛщУРөД»щұҫКВјюУРЈә
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬№І15ЦЦ.
Ј¬№І15ЦЦ.
КВјю![]() °ьә¬өД»щұҫКВјюУРЈә
°ьә¬өД»щұҫКВјюУРЈә
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬№І10ЦЦ.
Ј¬№І10ЦЦ.
ЛщТФХв2ёцәўЧУМшЙюКэЦө¶јФЪЗшјд![]() ДЪөДёЕВКОӘ
ДЪөДёЕВКОӘ![]() .
.