题目内容
关于x的不等式（k-1）x2+（k-3）x+（k-2）＞0的解是一切实数的条件________．
k
分析：分三种情况k-1=0，k-1＞0，k-1＜0讨论要使x取任意实数时，令f（x）=（k-1）x2+（k-3）x+（k-2）的增减性得到k的取值即可．
解答：①当k=1时，得到-2x-1＞0，解得x＜-
与解为一切实数矛盾，所以k≠1．
②当k-1＞0即k＞1时，设f（x）=（k-1）x2+（k-3）x+（k-2）为开口向上的抛物线，要使x取任意实数时，f（x）＞0即△＜0
即（k-3）2-4（k-1）（k-2）＜0解得：k＞
；
③当k-1＜0即k＜1时，f（x）=（k-1）x2+（k-3）x+（k-2）为开口向下的抛物线，要使x取任意实数时，f（x）＞0不成立．
综上，当k时，不等式的解是一切实数．
故答案为k
点评：考查学生利用分类讨论的数学思想解决问题的能力，理解函数恒成立时取条件的能力，以及研究二次函数图象性质的能力．
分析：分三种情况k-1=0，k-1＞0，k-1＜0讨论要使x取任意实数时，令f（x）=（k-1）x2+（k-3）x+（k-2）的增减性得到k的取值即可．
解答：①当k=1时，得到-2x-1＞0，解得x＜-
与解为一切实数矛盾，所以k≠1．②当k-1＞0即k＞1时，设f（x）=（k-1）x2+（k-3）x+（k-2）为开口向上的抛物线，要使x取任意实数时，f（x）＞0即△＜0
即（k-3）2-4（k-1）（k-2）＜0解得：k＞
；③当k-1＜0即k＜1时，f（x）=（k-1）x2+（k-3）x+（k-2）为开口向下的抛物线，要使x取任意实数时，f（x）＞0不成立．
综上，当k
时，不等式的解是一切实数．故答案为k
点评：考查学生利用分类讨论的数学思想解决问题的能力，理解函数恒成立时取条件的能力，以及研究二次函数图象性质的能力．
练习册系列答案
小学课时特训系列答案
相关题目
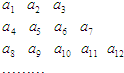将数列{an} 中的所有项按第一排三项，以下每一行比上一行多一项的规则排成如数表：记表中的第一列数a1，a4，a8，…构成的数列为{bn}，已知：