题目内容
4．
如图，经过圆锥顶点S的一个截面SAB和底面成60°的二面角，截底面所得弧长所对圆心角为120°，底面圆心O到截面SAB的距离为30cm，求棱锥S-OAB的体积．
分析 取AB的中点C，连接OC，SC，作OD⊥SC，则∠SCO=60°，OD=30cm，求出SO，OC，AB，即可求棱锥S-OAB的体积．
解答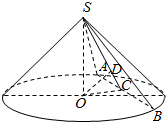 
解：取AB的中点C，连接OC，SC，作OD⊥SC，
则∠SCO=60°，OD=30cm，
∴SO=60cm，OC=20$\sqrt{3}$cm，
∵截底面所得弧长所对圆心角为120°，
∴AB=80$\sqrt{3}$cm，
∴棱锥S-OAB的体积=$\frac{1}{3}×\frac{1}{2}×80\sqrt{3}×20\sqrt{3}×60$=48000cm3．
点评 本题考查求棱锥S-OAB的体积，考查学生的计算能力，正确求出SO，OC，AB是关键．
练习册系列答案
相关题目
13．f（x0-0）与f（x0+0）的极限都存在是函数f（x）在点x0处有极限的（ ）
| A． | 必要条件 | B． | 充分条件 | C． | 充要条件 | D． | 无关条件 |
如图，已知圆的方程为x2+y2=$\frac{1}{2}$，椭圆方程为$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1，过原点的射线交圆于A，交椭圆于B，过A、B分别作x轴和y轴的平行线，求所作二直线交点P的轨迹方程．
如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，∠ABC=∠BCD=90°，面PAD⊥面ABCD，PA=PD=CD=BC=1，AB=2，AD=$\sqrt{2}$．