题目内容
13.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,准线方程为x=±4.(1)求椭圆C的方程;
(2)已知A为椭圆C上的左顶点,直线l过右焦点F2与椭圆C交于M,N两点,AM,AN的斜率k1,k2满足k1+k2=-$\frac{1}{2}$,求直线MN的方程.
分析 (1)利用椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,准线方程为x=±4,建立方程,求出a,b,由此能求出椭圆方程.
(2)设直线l为y=k(x-1),直线l和椭圆交于M(x1,y1),N(x2,y2).将y=k(x-1)代入3x2+4y2=12中,得(3+4k2)x2-8k2x+4k2-12=0,由此利用韦达定理能求出直线MN的方程.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,准线方程为x=±4,
∴$\frac{c}{a}$=$\frac{1}{2}$,$\frac{{a}^{2}}{c}$=4,
∴a=2,c=1,
∴b=$\sqrt{3}$,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1;…(6分)
(2)若直线l斜率不存在,显然k1+k2=0不合题意;…(8分)
则直线l的斜率存在.
设直线l为y=k(x-1),直线l和椭圆交于M(x1,y1),N(x2,y2).
将y=k(x-1)代入3x2+4y2=12中,得:(3+4k2)x2-8k2x+4k2-12=0,
依题意:△=9k2+9>0,…(10分)
由韦达定理知:x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
又kAM+kAN=$\frac{{y}_{1}}{{x}_{1}+2}$+$\frac{{y}_{2}}{{x}_{2}+2}$=k[2-3($\frac{1}{{x}_{1}+2}$+$\frac{1}{{x}_{2}+2}$)],
$\frac{1}{{x}_{1}+2}$+$\frac{1}{{x}_{2}+2}$=$\frac{{x}_{1}+{x}_{2}+4}{{x}_{1}{x}_{2}+2({x}_{1}+{x}_{2})+4}$=$\frac{8{k}^{2}+4(3+4{k}^{2})}{4{k}^{2}-12+16{k}^{2}+4(3+4{k}^{2})}$=$\frac{2{k}^{2}+1}{3{k}^{2}}$,
从而kAM+kAN=k(2-3•$\frac{2{k}^{2}+1}{3{k}^{2}}$)=-$\frac{1}{k}$=-$\frac{1}{2}$,…(14分)
解得k=2,符合△>0.
故所求直线MN的方程为:y=2(x-1).…(16分)
点评 本题考查椭圆方程的求法,考查直线方程的求法,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

| A. | an=$\frac{{n}^{2}-n+2}{2}$ | B. | an=$\frac{{n}^{2}-n+1}{2}$ | C. | an=$\frac{2}{{n}^{2}-n+1}$ | D. | an=$\frac{2}{{n}^{2}-n+2}$ |
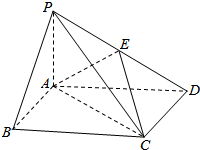 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.