题目内容

直线 $数学公式$ 与曲线y²=x只有一个公共点，则k=

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

B
分析：当斜率k=0 时，直线y=k（x+2）+ $\text{[math]}$ 平行于x轴，与抛物线y²=x仅有一个公共点，当斜率不等于0时，把y=k（x+2）+ $\text{[math]}$ 代入抛物线的方程化简，由判别式△=0求得实数k的值．
解答：当斜率k=0 时，直线y=k（x+2）+ $\text{[math]}$ 平行于x轴，与抛物线y²=x仅有一个公共点．
当斜率不等于0时，把y=k（x+2）+ $\text{[math]}$ 代入抛物线y²=x整理得ky²-y+2k+ $\text{[math]}$ =0．
由题意可得，此方程有唯一解，
故判别式△=1-4k（2k+ $\text{[math]}$ ）=0
∴k=- $\text{[math]}$ 或k= $\text{[math]}$ ，
综上得：k=0，- $\text{[math]}$ 或 $\text{[math]}$ ．
故选B．
点评：本题考查直线和圆锥曲线的位置关系，一元二次方程有唯一解的条件，体现了分类讨论的数学思想．本题的易错点在于忘记讨论k=0的情况，从而得到错误结论．

练习册系列答案

天利38套初中名校期末联考测试卷系列答案

捷径训练检测卷系列答案

成功一号名卷天下系列答案

小夫子全能检测系列答案

同步导练系列答案

卓越英语系列答案

时代新课程系列答案

核心考卷系列答案

精英教程100分攻略系列答案

轻轻松松系列答案

相关题目

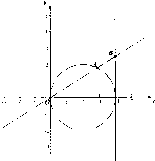已知点A（x₁，y₁）在圆（x-2）²+y²=4上运动，点A不与（0，0）重合，点B（4，y₀）在直线x=4上运动，动点M（x，y）满足

．动点M的轨迹C的方程为F（x，y）=0．
（1）试用点M的坐标x，y表示y₀，x₁，y₁；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由．（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）
①对称性；
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；
③图形范围；
④渐近线；
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性．

请考生注意：重点高中学生只做（1）、（2）两问，一般高中学生只做（1）、（3）两问．
已知P是圆F1：(x+1)2+y2=16上任意一点，点F₂的坐标为（1，0），直线m分别与线段F₁P、F₂P交于M、N两点，且

|．
（1）求点M的轨迹C的方程；
（2）斜率为k的直线l与曲线C交于P、Q两点，若

=0（O为坐标原点）．试求直线l在y轴上截距的取值范围；
（3）是否存在斜率为

的直线l与曲线C交于P、Q两点，使得

=0（O为坐标原点），若存在求出直线l的方程，否则说明理由．

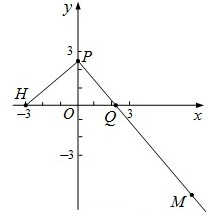（2009•卢湾区二模）如图，已知点H（-3，0），动点P在y轴上，点Q在x轴上，其横坐标不小于零，点M在直线PQ上，且满足

．
（1）当点P在y轴上移动时，求点M的轨迹C；
（2）过定点F（1，0）作互相垂直的直线l与l'，l与（1）中的轨迹C交于A、B两点，l'与（1）中的轨迹C交于D、E两点，求四边形ADBE面积S的最小值；
（3）（在下列两题中，任选一题，写出计算过程，并求出结果，若同时选做两题，
则只批阅第②小题，第①题的解答，不管正确与否，一律视为无效，不予批阅）：
①将（1）中的曲线C推广为椭圆：

+y2=1，并
将（2）中的定点取为焦点F（1，0），求与（2）相类似的问题的解；
②（解答本题，最多得9分）将（1）中的曲线C推广为椭圆：

=1，并
将（2）中的定点取为原点，求与（2）相类似的问题的解．

请考生注意：重点高中学生只做（1）、（2）两问，一般高中学生只做（1）、（3）两问．
已知P是圆F1：(x+1)2+y2=16上任意一点，点F₂的坐标为（1，0），直线m分别与线段F₁P、F₂P交于M、N两点，且

|．
（1）求点M的轨迹C的方程；
（2）斜率为k的直线l与曲线C交于P、Q两点，若

=0（O为坐标原点）．试求直线l在y轴上截距的取值范围；
（3）是否存在斜率为

的直线l与曲线C交于P、Q两点，使得

=0（O为坐标原点），若存在求出直线l的方程，否则说明理由．

已知点M（k，l）、P（m，n），（klmn≠0）是曲线C上的两点，点M、N关于x轴对称，直线MP、NP分别交x轴于点E（x_E，0）和点F（x_F，0），
（Ⅰ）用k、l、m、n分别表示x_E和x_F；
（Ⅱ）某同学发现，当曲线C的方程为：x²+y²=R²（R＞0）时，x_E·x_F=R²是一个定值与点M、N、P的位置无关；请你试探究当曲线C的方程为：

时，x_E·x_F的值是否也与点M、N、P的位置无关；
（Ⅲ）类比（Ⅱ）的探究过程，当曲线C的方程为y²=2px（p＞0）时，探究x_E与x_F经加、减、乘、除的某一种运算后为定值的一个正确结论。（只要求写出你的探究结论，无须证明）