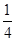题目内容
已知定义在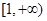 上的函数
上的函数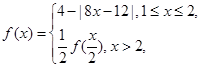 则
则
A.函数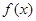 的值域为 的值域为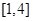 |
B.关于x的方程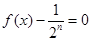 ( (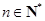 )有4个不相等的实数根 )有4个不相等的实数根 |
C.存在实数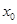 ,使得不等式 ,使得不等式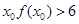 成立 成立 |
D.当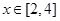 时,函数 时,函数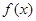 的图象与x轴围成的面积为1 的图象与x轴围成的面积为1 |
D
解析试题分析:当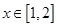 时
时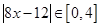
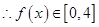 ,关于x的方程
,关于x的方程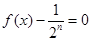 有2个实数根,当
有2个实数根,当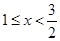 时
时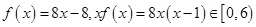 ,当
,当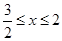 时
时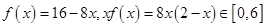 ,所以不存在实数
,所以不存在实数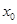 ,使得不等式
,使得不等式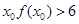 成立,
成立,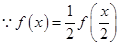 ,
,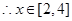 的函数值是
的函数值是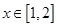 时函数值的一半,当
时函数值的一半,当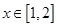 函数
函数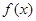 的图像与x轴围成的面积为
的图像与x轴围成的面积为 ,当
,当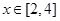 时,函数
时,函数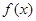 的图像与x轴围成的面积为1
的图像与x轴围成的面积为1
考点:函数图像与性质
点评:本题是函数性质的综合考查题,要求学生对函数图像及常用的性质要融会贯通,其中首要是分析清楚当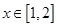 时函数分成两段来考虑其图像的具体情况
时函数分成两段来考虑其图像的具体情况

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数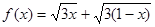 的最大值为
的最大值为
A.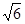 | B.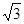 | C.3 | D.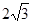 |
定义域为R的函数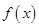 满足
满足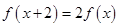 ,当
,当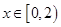 时,
时,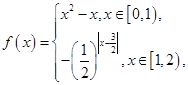 则当
则当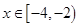 时,函数
时,函数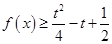 恒成立,则实数
恒成立,则实数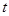 的取值范围为( )
的取值范围为( )
A.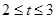 | B.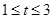 | C.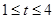 | D.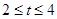 |
下列函数中,在 上为增函数的是 ( )
上为增函数的是 ( )
A. | B. | C. | D. |
若函数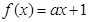 在R上递减,则函数
在R上递减,则函数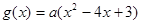 的增区间是 ( )
的增区间是 ( )
| A.(2,+∞) | B.(-∞,2) | C.(-2,+∞) | D.(-∞,-2) |
已知直线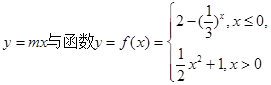 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )
A.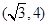 | B.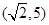 | C. | D. |
方程2x-x2=0的解的个数是( )
| A.1 | B.2 |
| C.3 | D.4 |
 记
记 ,则当
,则当 且
且 时,
时, 的大致图象为 ( )
的大致图象为 ( )
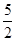 )=( )
)=( )