题目内容
【题目】中国在欧洲的某孔子学院为了让更多的人了解中国传统文化,在当地举办了一场由当地人参加的中国传统文化知识大赛,为了了解参加本次大赛参赛人员的成绩情况,从参赛的人员中随机抽取![]() 名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如下图所示,已知抽取的人员中成绩在[50,60)内的频数为3.
名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如下图所示,已知抽取的人员中成绩在[50,60)内的频数为3.

(1)求![]() 的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
(2)已知抽取的![]() 名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取1人,求这两人恰好都为女士的概率.
名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取1人,求这两人恰好都为女士的概率.
【答案】(1)![]() ;平均成绩73.75; (2)
;平均成绩73.75; (2)![]()
【解析】
(1)由频率之和等于1得出成绩在![]() 频率,结合该组频数,得出抽取的样本容量,再由频率分布直方图中的数据估计参赛人员的平均成绩即可;
频率,结合该组频数,得出抽取的样本容量,再由频率分布直方图中的数据估计参赛人员的平均成绩即可;
(2)由频率分布直方图得出成绩在![]() 和
和![]() 抽取的人数,设抽取的40人中成绩在
抽取的人数,设抽取的40人中成绩在![]() 之间男士为
之间男士为![]() ,女士为
,女士为![]() ,成绩在
,成绩在![]() 之间的男士为
之间的男士为![]() ,女士为
,女士为![]() ,列举出成绩在
,列举出成绩在![]() ,
,![]() 的被抽取人员中各随机选取1人的所有情况,利用古典概型概率公式求解即可.
的被抽取人员中各随机选取1人的所有情况,利用古典概型概率公式求解即可.
(1)由频率分布直方图知,成绩在![]() 频率为
频率为![]()
![]() 成绩在
成绩在![]() 内频数为3,
内频数为3,![]() 抽取的样本容量
抽取的样本容量![]()
![]() 参赛人员平均成绩为
参赛人员平均成绩为![]() .
.
(2)由频率分布直方图知,抽取的人员中成绩在![]() 的人数为
的人数为![]()
成绩在![]() 的人数为
的人数为![]()
设抽取的40人中成绩在![]() 之间男士为
之间男士为![]() ,女士为
,女士为![]()
成绩在![]() 之间的男士为
之间的男士为![]() ,女士为
,女士为![]()
从成绩在![]() ,
,![]() 的被抽取人员中各随机选取1人,有{
的被抽取人员中各随机选取1人,有{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },
},
{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() }
}
共有20种不同取法,其中选中的2人中恰好都为女士的取法有{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() }共4种不同取法,故选中的2人中恰好都为女士的概率为
}共4种不同取法,故选中的2人中恰好都为女士的概率为![]() .
.

【题目】某市食品药品监督管理局开展2020年春季快递餐饮安全检查,对本市的8个快递配餐点进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
快递配餐点编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分 | 82 | 75 | 70 | 66 | 83 | 93 | 95 | 100 |
卫生标准评分 | 81 | 79 | 77 | 75 | 82 | 83 | 84 | 87 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(精确到0.1)
的线性回归方程;(精确到0.1)
(2)现从8个被检查点中任意抽取两个组成一组,若两个点的原料采购加工标准和卫生标准的评分均超过80分,则组成“快递标兵配餐点”,求该组被评为“快递标兵配餐点”的概率.
参考公式: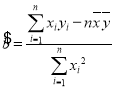 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.


