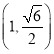题目内容
【题目】已知点![]() ,点
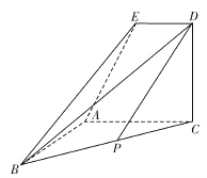
,点![]() 为动点,以
为动点,以![]() 为直径的圆内切于
为直径的圆内切于![]() .
.
(1)证明![]() 为定值,并求点
为定值,并求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
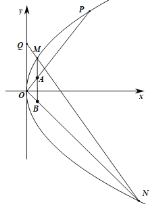
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,直线
两点,直线![]() 过点
过点![]() 且与
且与![]() 垂直,
垂直,![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() 为
为![]() 的中点,求
的中点,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由已知及椭圆的定义可得到点![]() 的轨迹方程;(2)设直线的方程
的轨迹方程;(2)设直线的方程![]() ,联立直线方程与椭圆方程,化为关于
,联立直线方程与椭圆方程,化为关于![]() 的一元二次方程,由根与系数关系表达三角形的底和高代入三角形的面积公式利用函数求最值.
的一元二次方程,由根与系数关系表达三角形的底和高代入三角形的面积公式利用函数求最值.
(1)设以![]() 为直径的圆的圆心为
为直径的圆的圆心为![]() ,半径为
,半径为![]() ,则
,则![]() ,
,
由![]()
所以,![]() 为定值,
为定值,
由![]()
所以,点![]() 的轨迹为以
的轨迹为以![]() ,
,![]() 为焦点的椭圆;
为焦点的椭圆;
则![]() ,
,![]() ,
,![]()
所以,点![]() 的轨迹方程为:
的轨迹方程为:![]() ;
;
(2)设![]()
由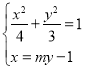 ,消去
,消去![]() 得,
得,![]()
易得,△![]() .
.
![]()
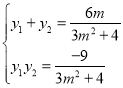
![]() 为
为![]() 的中点,
的中点,![]() ,
,![]()
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
又![]() 到
到![]() 的距离
的距离![]()
所以,![]()
设![]() ,则
,则![]()
所以,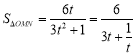
记![]() ,
,![]() 在
在![]() ,
,![]() 上递增,
上递增,![]() (1)
(1)![]() ,
,
所以,![]() 的最大值为
的最大值为![]() ,即,
,即,![]() 的面积的最大值为
的面积的最大值为![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
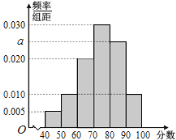
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |