题目内容
如图: △ABC的??ABC= 90°, V是平面ABC外的一点, VA = VB = VC = AC, 求VB与平面ABC所成的角。
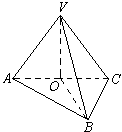
解析:
1、要求VB与平面ABC所成的角, 应作出它们所成的角。
2、要作出VB与平面ABC所成的角, 只要找出VB在平 面ABC内的射影就可以了。
3、作斜线在平面内的射影, 只要在斜线上找一点作直线 垂直于平面, 即找此点在平面内的射影, 显然找V点, V点在平面内的射影在何处?由条件可知, 射影为△ABC的外心。
解: 作VO^平面ABC于O, 则OB为VB在平面ABC内的射影,
∴??VBO为VB与平面ABC所成的角。
连OA、OB、OC, 则OA、OB、OC分别为斜线段VA、VB、VC在平面ABC内的射影。
∵VA = VB = VC
∴OA = OB = OC
∴O为△ABC为外心
∵△ABC为直角三角形, 且AC为斜边
∴O为AC的中点
设VA = a, 则VA = VC = AC = a, ![]()
在Rt△VOB中, 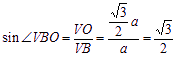
∴??VBO = 60°
∴VB与平面ABC所成的角为60°。

练习册系列答案
相关题目
 如图,△ABC的顶点A、B、C所对的边分别为a、b、c,A为圆心,直径PQ=2r,问:当P、Q取什么位置时,
如图,△ABC的顶点A、B、C所对的边分别为a、b、c,A为圆心,直径PQ=2r,问:当P、Q取什么位置时, 如图,△ABC的BC边的中点为M,利用向量证明:AB2+AC2=2(AM2+BM2).
如图,△ABC的BC边的中点为M,利用向量证明:AB2+AC2=2(AM2+BM2). (几何证明选讲选做题)如图,△ABC的外角平分线AD交外接圆于D,BD=4,则CD=
(几何证明选讲选做题)如图,△ABC的外角平分线AD交外接圆于D,BD=4,则CD=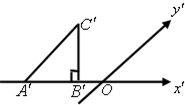 如图,△ABC的斜二侧直观图为等腰Rt△A'B'C',其中A'B'=2,则△ABC的面积为( )
如图,△ABC的斜二侧直观图为等腰Rt△A'B'C',其中A'B'=2,则△ABC的面积为( ) 如图,△ABC的外接圆⊙O的半径为
如图,△ABC的外接圆⊙O的半径为