题目内容
在△ABC中,a,b,c分别是角A、B、C所对的边,且b2=ac,向量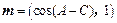 和
和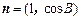 满足
满足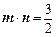 .
.
(1)求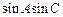 的值;
的值;
(2)三角形ABC为是否为等边三角形.
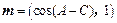 和
和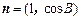 满足
满足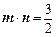 .
.(1)求
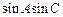 的值;
的值;(2)三角形ABC为是否为等边三角形.
(1)sinAsinC=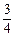 (2)三角形ABC为等边三角形
(2)三角形ABC为等边三角形
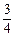 (2)三角形ABC为等边三角形
(2)三角形ABC为等边三角形(1)由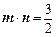 得,
得,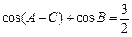 , ……………2分
, ……………2分
又B=π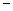 (A+C),得cos(A
(A+C),得cos(A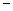 C)
C)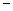 cos(A+C)=
cos(A+C)=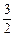 , …………4分
, …………4分
即cosAcosC+sinAsinC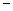 (cosAcosC
(cosAcosC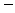 sinAsinC)=
sinAsinC)=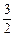 ,所以sinAsinC=
,所以sinAsinC=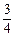 .…6分
.…6分
(2)由b2=ac及正弦定理得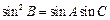 ,故
,故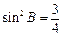 .……8分
.……8分
于是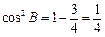 ,所以
,所以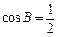 或
或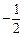 . 因为cosB =
. 因为cosB =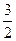
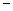 cos(A
cos(A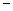 C)>0,
C)>0,
所以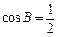 ,故
,故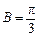 . ………………… 11分
. ………………… 11分
由余弦定理得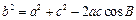 ,即
,即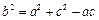 ,又b2=ac,
,又b2=ac,
所以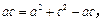 得a=c.
得a=c.
因为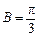 ,所以三角形ABC为等边三角形. ……… 14分
,所以三角形ABC为等边三角形. ……… 14分
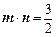 得,
得,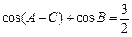 , ……………2分
, ……………2分又B=π
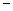 (A+C),得cos(A
(A+C),得cos(A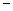 C)
C)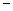 cos(A+C)=
cos(A+C)=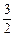 , …………4分
, …………4分即cosAcosC+sinAsinC
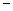 (cosAcosC
(cosAcosC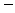 sinAsinC)=
sinAsinC)=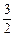 ,所以sinAsinC=
,所以sinAsinC=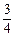 .…6分
.…6分(2)由b2=ac及正弦定理得
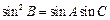 ,故
,故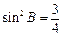 .……8分
.……8分于是
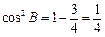 ,所以
,所以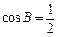 或
或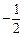 . 因为cosB =
. 因为cosB =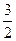
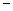 cos(A
cos(A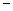 C)>0,
C)>0,所以
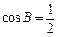 ,故
,故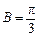 . ………………… 11分
. ………………… 11分由余弦定理得
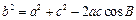 ,即
,即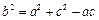 ,又b2=ac,
,又b2=ac,所以
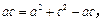 得a=c.
得a=c.因为
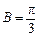 ,所以三角形ABC为等边三角形. ……… 14分
,所以三角形ABC为等边三角形. ……… 14分
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
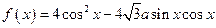 ,将
,将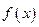 的图象先向右平移
的图象先向右平移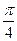 个单位,再向下平移2个单位后,所得到函数
个单位,再向下平移2个单位后,所得到函数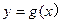 的图象关于直线
的图象关于直线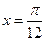 对称.
对称.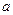 的值;
的值;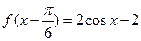 ,求
,求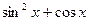 的值.
的值.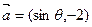 与
与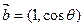 互相垂直,其中
互相垂直,其中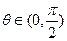 .
.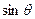 和
和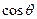 的值;(2)若
的值;(2)若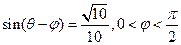 ,求
,求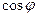 的值.
的值. 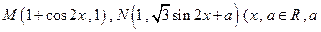 是常数
是常数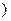 ,令
,令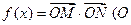 是坐标原点
是坐标原点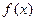 的解析式,并求函数
的解析式,并求函数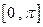 上的单调递增区间;
上的单调递增区间;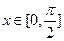 时,
时,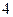 ,求a的值,并说明此时
,求a的值,并说明此时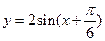 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到? ,求
,求 的值。
的值。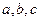 ,且
,且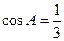 。
。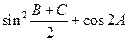 的值;(2)若
的值;(2)若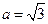 ,求
,求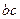 的最大值。
的最大值。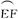 上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在
上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在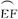 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?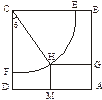
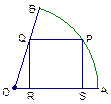
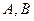 是单位圆上的两点,
是单位圆上的两点,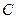 是圆与
是圆与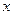 轴正半轴的交点,
轴正半轴的交点,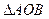 是正三角形,若点
是正三角形,若点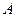 的坐标为
的坐标为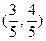 ,记
,记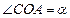 .
.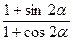 的值; (2)求
的值; (2)求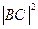 的值.
的值.